题目内容
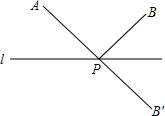 如图,点A、B在直线l的同侧,点B′是B点关于l的对称点,AB′交l于点P.
如图,点A、B在直线l的同侧,点B′是B点关于l的对称点,AB′交l于点P.(1)AB′与AP+PB相等吗?为什么?
(2)在l上再取一点Q,并连接AQ和QB,比较AQ+QB与AP+PB的大小,并说明理由.
考点:轴对称的性质
专题:
分析:(1)由轴对称的性质,对称点的连线被对称轴垂直平分,可得PB=PB′,即可得证AB′=AP+PB;
(2)连接QB′,由轴对称的性质可得:QB=QB′,然后根据两点之间线段最短(三角形的三边关系)可得:AQ+QB′>AB′,即AQ+QB>AP+PB.
(2)连接QB′,由轴对称的性质可得:QB=QB′,然后根据两点之间线段最短(三角形的三边关系)可得:AQ+QB′>AB′,即AQ+QB>AP+PB.
解答:解:(1)AB′与AP+PB相等,连接BB′,
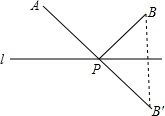
∵点B′是B点关于l的对称点,
∴l垂直平分线段BB′,
∴PB=PB′,
∴AP+PB′=AP+BP,
即:AB′=AP+BP;
(2)AQ+QB>AP+PB,
连接QB′,如图所示,
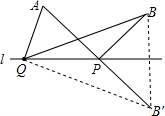
∵点B′是B点关于l的对称点,
∴l垂直平分线段BB′,
∴BQ=QB′,
∵AQ+QB′>AB′,
∴AQ+BQ>AB′,
∵AB′=AP+BP,
∴AQ+QB>AP+PB.

∵点B′是B点关于l的对称点,
∴l垂直平分线段BB′,
∴PB=PB′,
∴AP+PB′=AP+BP,
即:AB′=AP+BP;
(2)AQ+QB>AP+PB,
连接QB′,如图所示,

∵点B′是B点关于l的对称点,
∴l垂直平分线段BB′,
∴BQ=QB′,
∵AQ+QB′>AB′,
∴AQ+BQ>AB′,
∵AB′=AP+BP,
∴AQ+QB>AP+PB.
点评:本题考查的是轴对称--最短路线的问题,涉熟知两点之间线段最短(三角形任意两边之和大于第三边)的知识是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,具有过原点,且当x>0时,y随x增大而减小,这两个特征的有( )
①y=-ax2(a>0);②y=(a-1)x2(a<1);③y=-2x+a2(a≠0);④y=
x-a(a≠0).
①y=-ax2(a>0);②y=(a-1)x2(a<1);③y=-2x+a2(a≠0);④y=
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列说法:①有两个底角相等的梯形是等腰梯形;②有两边相等的梯形是等腰梯形;③两条对角线相等的梯形是等腰梯形;④等腰梯形上下底中点连线段把梯形分成面积相等的两部分,其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、5个 |
函数y=ax2与y=-ax+b的图象可能是( )
A、 |
B、 |
C、 |
D、 |
半径为R的⊙O中,弦AB=2R,弦CD=R,若两弦的弦心距分别为OE、OF,则OE:OF( )
| A、2:1 | B、3:2 |
| C、2:3 | D、0 |
 如图,在平面直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1). 我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”为一次变换.
如图,在平面直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1). 我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”为一次变换.