题目内容
 如图,等腰△ACB中,AB=AC.直线AD是它的对称轴;DE⊥AC于E,DF⊥AB于F,则图中直角三角形有
如图,等腰△ACB中,AB=AC.直线AD是它的对称轴;DE⊥AC于E,DF⊥AB于F,则图中直角三角形有考点:轴对称的性质
专题:
分析:先根据等腰三角形三线合一的性质得出AD⊥BC,故可得出直角三角形,再由全等三角形的判定定理得出全等的三角形,由轴对称的性质得出F点关于AD成轴对称的对应点.
解答:解:∵等腰△ACB中,AB=AC.直线AD是它的对称轴,
∴AD⊥BC.
∵DE⊥AC于E,DF⊥AB于F,
∴图中直角三角形有△ABD,△ACD,△ADF,△ADE,△BDF,△CDE,共6个;
∵等腰△ACB中,AB=AC,AD⊥BC,
∴在Rt△ABD与Rt△ACD中,
∵
,
∴△ABD≌△ACD(HL).
同理,△ADF≌△ADE,△BDF≌△CDE,
∴全等的三角形有3对.
∵△BDF≌△CDE,
∴BE=CE,
∴F点关于AD成轴对称的对应点是E点.
故答案为:6,3,E.
∴AD⊥BC.
∵DE⊥AC于E,DF⊥AB于F,
∴图中直角三角形有△ABD,△ACD,△ADF,△ADE,△BDF,△CDE,共6个;
∵等腰△ACB中,AB=AC,AD⊥BC,
∴在Rt△ABD与Rt△ACD中,
∵
|
∴△ABD≌△ACD(HL).
同理,△ADF≌△ADE,△BDF≌△CDE,
∴全等的三角形有3对.
∵△BDF≌△CDE,
∴BE=CE,
∴F点关于AD成轴对称的对应点是E点.
故答案为:6,3,E.
点评:本题考查的是轴对称的性质,熟知如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线是解答此题的关键.

练习册系列答案
相关题目
下列函数中,具有过原点,且当x>0时,y随x增大而减小,这两个特征的有( )
①y=-ax2(a>0);②y=(a-1)x2(a<1);③y=-2x+a2(a≠0);④y=
x-a(a≠0).
①y=-ax2(a>0);②y=(a-1)x2(a<1);③y=-2x+a2(a≠0);④y=
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
函数y=ax2与y=-ax+b的图象可能是( )
A、 |
B、 |
C、 |
D、 |
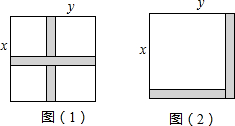 如图(1)、(2)某小区规划在边长为x米的正方形场地上修建两条宽为y米的人行道,其余部分种草,请你用不同的方法表示出草坪所占的面积,从中你发现了什么数学公式?请写出来.
如图(1)、(2)某小区规划在边长为x米的正方形场地上修建两条宽为y米的人行道,其余部分种草,请你用不同的方法表示出草坪所占的面积,从中你发现了什么数学公式?请写出来. 如图,在平面直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1). 我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”为一次变换.
如图,在平面直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1). 我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”为一次变换.