题目内容
某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(100-x)件.设这段时间内售出该商品的利润为y元.
(1)直接写出利润y与售价x之间的函数关系式;
(2)当售价为多少元时,利润可达1000元;
(3)应如何定价才能使利润最大?
(1)直接写出利润y与售价x之间的函数关系式;
(2)当售价为多少元时,利润可达1000元;
(3)应如何定价才能使利润最大?
考点:二次函数的应用
专题:
分析:(1)利用销量×每件利润进而得出y与x的函数关系式;
(2)利用y=1000,解方程求出即可;
(3)利用配方法求二次函数最值方法得出即可.
(2)利用y=1000,解方程求出即可;
(3)利用配方法求二次函数最值方法得出即可.
解答:解:(1)由题意可得:y=(x-30)(100-x)=-x2+130x-3000;
(2)令-x2+130x-3000=1000,
解得:x1=50,x2=80,
答:当售价为50元/件或80元/件时,利润可达1000元;
(3)由题意可得:
y=-x2+130x-3000
=-(x-65)2+1225,
当x=65时,函数有最大值1225,
答:当定价为65元/件时,利润最大.
(2)令-x2+130x-3000=1000,
解得:x1=50,x2=80,
答:当售价为50元/件或80元/件时,利润可达1000元;
(3)由题意可得:
y=-x2+130x-3000
=-(x-65)2+1225,
当x=65时,函数有最大值1225,
答:当定价为65元/件时,利润最大.
点评:此题主要考查了二次函数的应用以及一元二次方程的应用,正确得出y与x的函数关系式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,具有过原点,且当x>0时,y随x增大而减小,这两个特征的有( )
①y=-ax2(a>0);②y=(a-1)x2(a<1);③y=-2x+a2(a≠0);④y=
x-a(a≠0).
①y=-ax2(a>0);②y=(a-1)x2(a<1);③y=-2x+a2(a≠0);④y=
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
拱桥呈抛物线型,其函数解析式为y=-
x2,当拱桥下水面宽为12m时,水面离拱桥顶端的高度h是( )
| 1 |
| 4 |
| A、3m | ||
B、2
| ||
C、4
| ||
| D、9m |
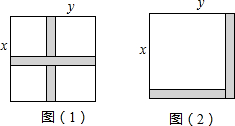 如图(1)、(2)某小区规划在边长为x米的正方形场地上修建两条宽为y米的人行道,其余部分种草,请你用不同的方法表示出草坪所占的面积,从中你发现了什么数学公式?请写出来.
如图(1)、(2)某小区规划在边长为x米的正方形场地上修建两条宽为y米的人行道,其余部分种草,请你用不同的方法表示出草坪所占的面积,从中你发现了什么数学公式?请写出来. 如图,在平面直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1). 我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”为一次变换.
如图,在平面直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1). 我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”为一次变换.