题目内容
5．先化简，再求值：$\frac{1}{a-2}$÷$\frac{{a}^{2}+4a+4}{{a}^{2}-4}$，其中a=4．分析 先将原式化简，然后将a的值代入即可求出答案．
解答 解：原式=$\frac{1}{a-2}$÷$\frac{（a+2）^{2}}{（a+2）（a-2）}$
=$\frac{1}{a-2}$•$\frac{（a+2）（a-2）}{（a+2）^{2}}$
=$\frac{1}{a+2}$
当a=4时，
∴原式=$\frac{1}{6}$
点评 本题考查分式的化简求值，解题的关键是熟练运用分式的运算法则，本题属于基础题型．
练习册系列答案
名校课堂系列答案
相关题目
16．有一组数据：3，5，5，6，7，对这组数据分析错误的是（ ）
| A． | 众数是5 | B． | 中位数是5 | C． | 平均数是5 | D． | 极差是4 |
20．
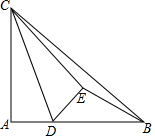如图，在Rt△ABC中，∠A=90°，AB=4，AC=3，D为AB上一动点，将△ACD沿CD翻折得到△ECD，那么BE的最小值为（ ）
如图，在Rt△ABC中，∠A=90°，AB=4，AC=3，D为AB上一动点，将△ACD沿CD翻折得到△ECD，那么BE的最小值为（ ）| A． | $\sqrt{3}$ | B． | 4-$\sqrt{3}$ | C． | $\sqrt{5}$ | D． | 2 |
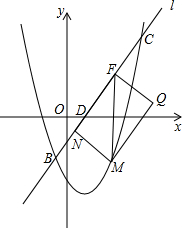已知抛物线y=ax2+bx+c（a≠0）经过原点，顶点为A（h，k）（h≠0）．
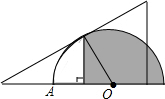如图，将一块含30°角的直角三角版和半圆量角器按如图的方式摆放，使斜边与半圆相切．若半径OA=4，则图中阴影部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$．（结果保留π）