题目内容
17. 已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线y=tx2(t≠0)也经过点A,过a与t之间的关系式;
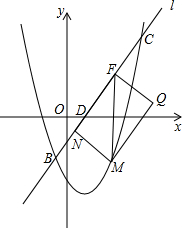
(3)在(2)的条件下,已知a=-$\frac{1}{2}$,直线l:y=$\frac{4}{3}$x-1与抛物线y=tx2-$\frac{2}{3}$x-7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2-$\frac{2}{3}$x-7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值.
分析 (1)设抛物线的解析式为顶点式,再把原点坐标代入可求得a的值,可求得抛物线解析式;
(2)把A点坐标分别代入两抛物线解析式,把原点坐标代入整理可得到a与t之间的函数关系式;
(3)利用(2)的结论可求得a和t的值,可用m表示出M、F的坐标,从而可用m表示出FM,由条件可求得OD、OE和DE的长,在矩形MNFQ中,利用三角函数的定义可用MF表示出NF和MN,从而可表示出P,再利用二次函数的性质可求得其最大值.
解答 解:
(1)∵由题意可知抛物线顶点坐标为(1,2),
∴可设抛物线解析式为y=a(x-1)2+2,
∵抛物线过原点,
∴0=a(0-1)2+2,解得a=-2,
∴抛物线解析式为y=-2(x-1)2+2;
(2)∵抛物线y=tx2(t≠0)也经过点A,
∴k=th2,
∴y=a(x-h)2+k=a(x-h)2+th2,
∵当x=0时y=0,
∴0=ah2+th2,
∵h≠0,
∴a+t=0,即a=-t;
(3)由(2)可知a=-t,
∴当a=-$\frac{1}{2}$时,t=$\frac{1}{2}$,
∴M(m,$\frac{1}{2}$m2-$\frac{2}{3}$m-7),F(m,$\frac{4}{3}$m-1),
∴FM=($\frac{4}{3}$m-1)-($\frac{1}{2}$m2-$\frac{2}{3}$m-7)=-$\frac{1}{2}$m2+2m+6,
又在y=$\frac{4}{3}$x-1中,当x=0时,y=-1,y=0时x=$\frac{3}{4}$,
∴OD=$\frac{3}{4}$,OE=1,
∴DE=$\sqrt{O{D}^{2}+O{E}^{2}}$=$\frac{5}{4}$,
∵MF∥y轴,
∴∠DEO=∠MFN,
在矩形MNFQ中,NF=MF•cos∠MFN=MF•$\frac{OE}{DE}$=$\frac{4}{5}$MF,
MN=MF•sin∠MFN=MF•$\frac{OD}{DE}$=$\frac{3}{5}$MF,
∴P=2(MN+NF)=$\frac{14}{5}$MF=$\frac{14}{5}$(-$\frac{1}{2}$m2+2m+6)=-$\frac{7}{5}$m2+$\frac{28}{5}$m+$\frac{84}{5}$=-$\frac{7}{5}$(m-2)2+$\frac{112}{5}$,
∵0<m<6,-$\frac{7}{5}$<0,
∴当m=2时,P取最大值,最大值为$\frac{112}{5}$.
点评 本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、勾股定理、三角函数的定义、矩形的性质等知识.在(1)中注意设为顶点式,在(2)中利用两抛物线都过A点消去k是解题的关键,在(3)中用MF分别表示出NF和MN是解题的关键.本题考查知识点较多,综合性较强,难度较大.

| A. | ①②③④ | B. | ①②④ | C. | ①②③ | D. | ①② |
 如图是某个几何体的三视图,该几何体为( )
如图是某个几何体的三视图,该几何体为( )| A. | 长方体 | B. | 四面体 | C. | 圆柱体 | D. | 四棱锥 |

| A. | 四棱柱 | B. | 三棱柱 | C. | 三棱锥 | D. | 圆锥 |

 在⊙O中,AB是直径,AC是切线且AC=AB,联结BC交⊙O于点D,试仅用无刻度直尺,作以D为切点的⊙O的切线DT.
在⊙O中,AB是直径,AC是切线且AC=AB,联结BC交⊙O于点D,试仅用无刻度直尺,作以D为切点的⊙O的切线DT.
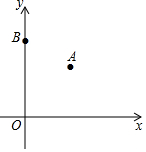 如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )
如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )