��Ŀ����
13����֪�߶�MN=8��C���߶�MN��һ���㣬��MN��ͬ��ֱ����ȱߡ�CMD�͵ȱߡ�CNE����1����ͼ�٣�����DN��EM�������߶��ཻ�ڵ�H����֤ME=DN�������DHM�Ķ�����
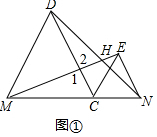
��2����ͼ�ڣ�����D��E�ֱ����߶�MN�Ĵ��ߣ�����ֱ�ΪF��G���ʣ��ڵ�C�˶������У�DF+EG�ij����Ƿ�Ϊ��ֵ������ǣ�����������ֵ�����������˵�����ɣ�
��3������C�ɵ�M�Ƶ���Nʱ����H�Ƶ���·������Ϊ$\frac{16\sqrt{3}}{9}$�У�ֱ��д�������
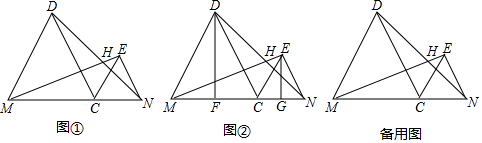
���� ��1�����ݵȱ������ε����ʵõ�CM=CD��EC=NC����DCM=��ECN=60�㣬����ȫ�������ε����ʵõ�ME=DN����CME=��CDN�����������ε��ڽǺ͵õ���DHM=��DCM=60�㣻
��2����MF=FC=x����CG=NG=4-x���õ�DF=$\sqrt{3}$x��EG=$\sqrt{3}$��4-x�������ɵõ����ۣ�
��3����ͼ�ۣ�����C�ɵ�M�Ƶ���Nʱ����H�ƶ���·����Ϊ$\widehat{MHN}$�������ڲ��ǵĶ���õ���MHN=120�㣬����Բ�ܽǶ���õ���MON=120�㣬��ֱ�������εõ�OM=ON=$\frac{8\sqrt{3}}{3}$�����ǵõ����ۣ�
���  ��1��֤�����ߡ�CMD���CNE�ǵȱ������Σ�
��1��֤�����ߡ�CMD���CNE�ǵȱ������Σ�
��CM=CD��EC=NC����DCM=��ECN=60�㣬
���DCN=��MCE=120�㣬
�ڡ�MCE���DCN�У�$\left\{\begin{array}{l}{MC=DC}\\{��MCE=��DCN}\\{EC=NC}\end{array}\right.$��
���MCE�ա�DCN��
��ME=DN����CME=��CDN��
�ߡ�1=��2��
��180��-��CME-��1=180��-��CDN-��2��
���DHM=��DCM=60�㣻
��2���⣺DF+EGΪ��ֵ��
���ɣ���MF=FC=x����CG=NG=4-x��
��DF=$\sqrt{3}$x��EG=$\sqrt{3}$��4-x����
��DF+GE=$\sqrt{3}$x+$\sqrt{3}$��4-x��=4$\sqrt{3}$��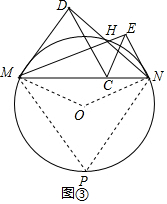
��3���⣺��ͼ�ۣ�����C�ɵ�M�Ƶ���Nʱ����H�Ƶ���·����Ϊ$\widehat{MHN}$��
�ߡ�MHD=60�㣬
���MHN=120�㣬
���MPN=60�㣬
���MON=120�㣬
��MN=8��
��OM=ON=$\frac{8\sqrt{3}}{3}$��
���H�Ƶ���·������=$\frac{120�С�\frac{8\sqrt{3}}{3}}{180}$=$\frac{16\sqrt{3}��}{9}$��
�ʴ�Ϊ��$\frac{16\sqrt{3}��}{9}$��
���� ���⿼����ȫ�������ε��ж������ʣ��ȱ������ε����ʣ�Բ�ڽ��ı��ε����ʣ�Բ�ܽǶ�������ȷ������ͼ���ǽ���Ĺؼ���

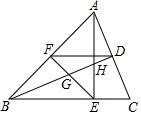 ��ͼ���ڡ�ABC�У�AE��BD�Ǹߣ���ABE=45�㣬��F��AB���е㣬BD��FE��AE�ֱ��ڵ�G��H����CAE=��ABD�������н��ۣ���FD=FE����BH=2CD����BD•BH=2BE2����S��ABC=$\frac{4}{3}$S�ı���BCDF��������ȷ���У�������
��ͼ���ڡ�ABC�У�AE��BD�Ǹߣ���ABE=45�㣬��F��AB���е㣬BD��FE��AE�ֱ��ڵ�G��H����CAE=��ABD�������н��ۣ���FD=FE����BH=2CD����BD•BH=2BE2����S��ABC=$\frac{4}{3}$S�ı���BCDF��������ȷ���У�������| A�� | �٢� | B�� | �ڢ� | C�� | �٢ڢ� | D�� | �٢ڢ� |
| A�� | x=-1 | B�� | x=1 | C�� | x=-2 | D�� | x=2 |
 ij��������ͼ��ʾ���ü����������ͼ�ǣ�������
ij��������ͼ��ʾ���ü����������ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� | �٢ڢۢ� | B�� | �٢ڢ� | C�� | �٢ڢ� | D�� | �٢� |
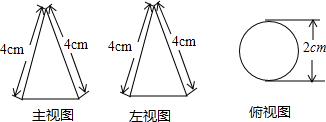
| A�� | 2��cm2 | B�� | 4��cm2 | C�� | 8��cm2 | D�� | 16��cm2 |
 �ڡ�O�У�AB��ֱ����AC��������AC=AB������BC����O�ڵ�D���Խ����̶�ֱ�ߣ�����DΪ�е�ġ�O������DT��
�ڡ�O�У�AB��ֱ����AC��������AC=AB������BC����O�ڵ�D���Խ����̶�ֱ�ߣ�����DΪ�е�ġ�O������DT��