题目内容

15．计算：$\sqrt{（a-\frac{1}{a}）^{2}}$-$\sqrt{（a+\frac{1}{a}）^{2}}$（0＜a＜1）

分析 根据a的取值范围化简二次根式．

解答 解：∵0＜a＜1，
∴0＜a＜1＜$\frac{1}{a}$，
∴a-$\frac{1}{a}$＜0，a+$\frac{1}{a}$＞0，
∴$\sqrt{（a-\frac{1}{a}）^{2}}$-$\sqrt{（a+\frac{1}{a}）^{2}}$
=|a-$\frac{1}{a}$|-|a+$\frac{1}{a}$|
=$\frac{1}{a}$-a-a-$\frac{1}{a}$
=-2a．

点评 本题主要考查了二次根式的化简，根据题意得到a-$\frac{1}{a}$＜0，a+$\frac{1}{a}$＞0是解题的难点．

练习册系列答案
相关题目
5．已知多项式x2+2y2-4x+4y+10，其中x，y为任意实数，那么当x，y分别取何值时，多项式的值达到最小值，最小值为（　　）
A．2B．$\frac{5}{2}$C．4D．10
6．由方程组$\left\{\begin{array}{l}{x+m=6}\\{y-m=3}\end{array}\right.$可以得出x、y的关系式是（　　）
A．x+y=3B．x+y=-3C．x+y=-9D．x+y=9
3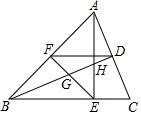．如图，在△ABC中，AE和BD是高，∠ABE=45°，点F是AB的中点，BD与FE，AE分别交于点G、H，∠CAE=∠ABD．有下列结论：①FD=FE；②BH=2CD；③BD•BH=2BE2；④S△ABC=$\frac{4}{3}$S四边形BCDF．其中正确的有（　　）
A．①③B．②④C．①②③D．①②④
10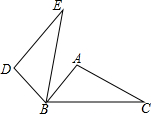．如图，△ABC中，∠ABC=50°，∠C=30°，将△ABC绕点B逆时针旋转α（0°＜α≤90°）得到△DBE，若DE∥AB，则α为（　　）
A．50°B．70°C．80°D．90°
20．在平面直角坐标系中，点A与点B关于x轴对称，若点A的坐标为（2，3），则点B所在的象限是（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
7．在平面直角坐标系中，M（3，0）、N（-1，0）、C（0，1）．若点A在线段MN上运动，△ABC是直角三角形．且∠ACB=90°，
①当∠B=45°时（如图1），画出点B的运动路径，并求其路径的长；
②当∠B=30°时（如图2），直接写出点B的运动路径的长．
4．分式方程$\frac{2}{x}$-$\frac{x-1}{x}$=2的解是（　　）
A．x=-1B．x=1C．x=-2D．x=2
5．先化简，再求值：$\frac{1}{a-2}$÷$\frac{{a}^{2}+4a+4}{{a}^{2}-4}$，其中a=4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网