题目内容
15.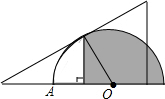 如图,将一块含30°角的直角三角版和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=4,则图中阴影部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$.(结果保留π)
如图,将一块含30°角的直角三角版和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=4,则图中阴影部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$.(结果保留π)
分析 求出OC=$\frac{1}{2}$OB=2,BC=2$\sqrt{3}$,图中阴影部分的面积=扇形BOD的面积+△BOC的面积.
解答 解:如图所示:
∵斜边与半圆相切,点B是切点,
∴∠EBO=90°.
又∵∠E=30°,
∴∠EBC=60°.
∴∠BOD=120°,
∵OA=OB=4,
∴OC=$\frac{1}{2}$OB=2,BC=2$\sqrt{3}$.
∴S阴影=S扇形BOD+S△BOC=$\frac{120π×{4}^{2}}{360}$+$\frac{1}{2}$×2×2$\sqrt{3}$=$\frac{16π}{3}$+2$\sqrt{3}$.
故答案为:$\frac{16π}{3}$+2$\sqrt{3}$.
点评 本题考查了切线的性质,扇形面积的计算.此题利用了“分割法”求得阴影部分的面积.

练习册系列答案
相关题目
6.如图是一个几何体的三视图,这个几何体是( )


| A. | 四棱柱 | B. | 三棱柱 | C. | 三棱锥 | D. | 圆锥 |
3.一个几何体的三视图如图所示,该几何体的侧面积为( )
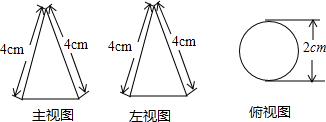

| A. | 2πcm2 | B. | 4πcm2 | C. | 8πcm2 | D. | 16πcm2 |
10.下列四个几何体中,主视图为圆的是( )
| A. | 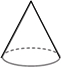 | B. |  | C. | 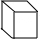 | D. |  |
4.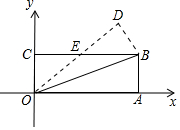 如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
 如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )| A. | $y=\frac{4}{5}x$ | B. | $y=\frac{5}{4}x$ | C. | $y=\frac{3}{4}x$ | D. | $y=\frac{4}{3}x$ |
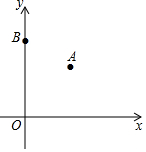 如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )
如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( ) 如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.