题目内容
8.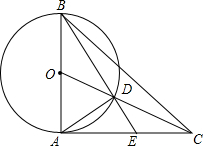 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )| A. | BD=$\frac{2}{3}$BC | B. | AD=OD | C. | AD=CD | D. | AE=CD |
分析 设⊙O的半径为a,则AB=2a,AC=2a,根据勾股定理得到OC=$\sqrt{O{A}^{2}+A{C}^{2}}=\sqrt{{a}^{2}+(2a)^{2}}=\sqrt{5}a$,求得CD=$\sqrt{5}a-a$,作DM⊥AC于点M,DN⊥AB于点N,根据相似三角形的性质得到$\frac{OD}{OC}=\frac{DN}{AC}$=$\frac{ON}{OA}$,得到DN=$\frac{2}{\sqrt{5}}$a,ON=$\frac{1}{\sqrt{5}}$a,于是得到BN=$\frac{\sqrt{5}+1}{5}$a,求得AE=$\sqrt{5}a-a$,即可得到结论.
解答  解:设⊙O的半径为a,则AB=2a,AC=2a,
解:设⊙O的半径为a,则AB=2a,AC=2a,
∵∠OAC=90°,
∴OC=$\sqrt{O{A}^{2}+A{C}^{2}}=\sqrt{{a}^{2}+(2a)^{2}}=\sqrt{5}a$,
∵OD=a,
∴CD=$\sqrt{5}a-a$,
作DM⊥AC于点M,DN⊥AB于点N,
∵∠BAC=90°,
∴DN∥AC,
∴△ODN∽△OAC,
∴$\frac{OD}{OC}=\frac{DN}{AC}$=$\frac{ON}{OA}$,
∴DN=$\frac{2}{\sqrt{5}}$a,ON=$\frac{1}{\sqrt{5}}$a,
∴BN=$\frac{\sqrt{5}+1}{5}$a,
∵△BDN∽△BEA,
∴$\frac{BN}{AB}=\frac{DN}{AE}$,
∴AE=$\sqrt{5}a-a$,
∴CD=AE,
故选D.
点评 本题考查了圆的性质,相似三角形的判定和性质,勾股定理,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
18.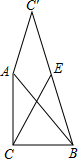 如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
 如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{2}$+1 | C. | $\frac{\sqrt{2}}{2}$+1 | D. | $\frac{\sqrt{5}}{2}$+1 |
13.在1,0,π,-3这四个数中,最大的数是( )
| A. | 1 | B. | 0 | C. | π | D. | -3 |
18.用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
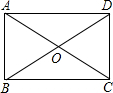 如图,在矩形ABCD中,对角线AC、BD交于点O,已知∠AOB=60°,AC=6,则矩形ABCD的面积是9$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC、BD交于点O,已知∠AOB=60°,AC=6,则矩形ABCD的面积是9$\sqrt{3}$.
 如图,在海中有一个小岛A,在它周围6n mile内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得小岛A在北偏东55方向,航行6n mlie到达C点,这时测得小岛A在北偏东29°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险.参考数据:tan29°≈0.55,tan35°≈0.70,tan55°≈1.43,tan61°≈1.80.
如图,在海中有一个小岛A,在它周围6n mile内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得小岛A在北偏东55方向,航行6n mlie到达C点,这时测得小岛A在北偏东29°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险.参考数据:tan29°≈0.55,tan35°≈0.70,tan55°≈1.43,tan61°≈1.80.