题目内容
18.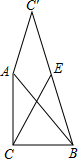 如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{2}$+1 | C. | $\frac{\sqrt{2}}{2}$+1 | D. | $\frac{\sqrt{5}}{2}$+1 |
分析 取AB的中点M,连接CM,EM,当CE=CM+EM时,CE的值最大,根据旋转的性质得到AC′=AC=2,由三角形的中位线的性质得到EM=$\frac{1}{2}$AC′=1,根据勾股定理得到AB=2$\sqrt{2}$,即可得到结论.
解答 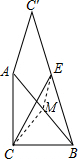 解:取AB的中点M,连接CM,EM,
解:取AB的中点M,连接CM,EM,
∴当CE=CM+EM时,CE的值最大,
∵将直角边AC绕A点逆时针旋转至AC′,
∴AC′=AC=2,
∵E为BC′的中点,
∴EM=$\frac{1}{2}$AC′=1,
∵∠ACB=90°,AC=BC=2,
∴AB=2$\sqrt{2}$,
∴CM=$\frac{1}{2}$AB=$\sqrt{2}$,
∴CE=CM+EM=$\sqrt{2}+1$,
故选B.
点评 本题考查了旋转的性质,直角三角形的性质,三角形的中位线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.式子$\frac{\sqrt{2x+1}}{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x≥-$\frac{1}{2}$且x≠1 | C. | x≥-$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$且x≠1 |
9.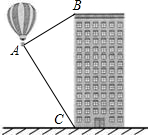 如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )
如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )
 如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )
如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )| A. | 15$\sqrt{3}$ | B. | 30$\sqrt{3}$ | C. | 45$\sqrt{3}$ | D. | 60$\sqrt{3}$ |
6.下列叙述中正确的是( )
| A. | (-11)2的算术平方根是±11 | |
| B. | 大于零而小于1的数的算术平方根比原数大 | |
| C. | 大于零而小于1的数的平方根比原数大 | |
| D. | 任何一个非负数的平方根都是非负数 |
13.据统计,2015年我国高新技术产品出口总额约为40590亿元,40590亿这个数用科学记数法表示为( )
| A. | 4.0590×109 | B. | 0.40590×1010 | C. | 40.590×1011 | D. | 4.0590×1012 |
3.设关于x的方程x2+px+q+1=0的两个实数根是m、n(m<n),关于x的方程x2+px+q-4=0的两个实数根是d、e(d<e),则m、n、d、e的大小关系是( )
| A. | m<d<e<n | B. | m<d<n<e | C. | d<m<e<n | D. | d<m<n<e |
7.-2的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
8.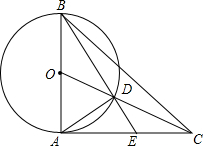 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )| A. | BD=$\frac{2}{3}$BC | B. | AD=OD | C. | AD=CD | D. | AE=CD |