题目内容
19.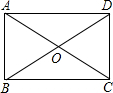 如图,在矩形ABCD中,对角线AC、BD交于点O,已知∠AOB=60°,AC=6,则矩形ABCD的面积是9$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC、BD交于点O,已知∠AOB=60°,AC=6,则矩形ABCD的面积是9$\sqrt{3}$.
分析 根据矩形性质得出∠ABC=90°,OA=OB=OC=OD,得出等边三角形AOB,求出AB=OA=3,根据勾股定理求出BC,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC=6,OA=OC=$\frac{1}{2}$AC=3,BO=OD=$\frac{1}{2}$BD=3,
∴OA=OB=OC=OD,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB=3,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴矩形ABCD的面积=AB•BC=3×3$\sqrt{3}$=9$\sqrt{3}$;
故答案为:9$\sqrt{3}$.
点评 本题考查了矩形性质,等边三角形的性质和判定,勾股定理等知识点熟练掌握矩形的性质,证明三角形AOB是等边三角形是解决问题的关键.

练习册系列答案
相关题目
9.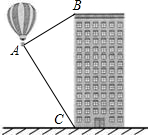 如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )
如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )
 如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )
如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )| A. | 15$\sqrt{3}$ | B. | 30$\sqrt{3}$ | C. | 45$\sqrt{3}$ | D. | 60$\sqrt{3}$ |
7.-2的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
14.下列由左边到右边的变形,属于分解因式的变形是( )
| A. | ab+ac+d=a(b+c)+d | B. | a2-1=(a+1)(a-1) | C. | 12ab2c=3ab•4bc | D. | (a+1)(a-1)=a2-1 |
4.下面是我国几家银行的标志,其中既是轴对称图形,又是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.分别过一个三角形的3个顶点作对边的平行线,这些平行线两两相交,则构成的平行四边形的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.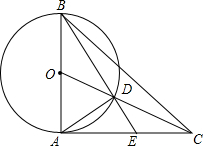 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )| A. | BD=$\frac{2}{3}$BC | B. | AD=OD | C. | AD=CD | D. | AE=CD |
9. 如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )
如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )
 如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )
如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |