题目内容
3. 如图,在海中有一个小岛A,在它周围6n mile内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得小岛A在北偏东55方向,航行6n mlie到达C点,这时测得小岛A在北偏东29°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险.参考数据:tan29°≈0.55,tan35°≈0.70,tan55°≈1.43,tan61°≈1.80.
如图,在海中有一个小岛A,在它周围6n mile内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得小岛A在北偏东55方向,航行6n mlie到达C点,这时测得小岛A在北偏东29°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险.参考数据:tan29°≈0.55,tan35°≈0.70,tan55°≈1.43,tan61°≈1.80.
分析 作AE⊥BC,交BC的延长线于E,设AE为xnmile,根据正切的概念用x分别表示出BE、CE,根据题意列出方程,解方程即可.
解答 解:作AE⊥BC交BC的延长线于点E. 设AE=x6n mile,
设AE=x6n mile,
∵在Rt△ABE中,∠B=90°-55°=35°,
tanB=$\frac{AE}{BE}$,
则BE=$\frac{AE}{tanB}$=$\frac{x}{0.7}$=$\frac{10x}{7}$,
在Rt△ACE中,∠ACE=90°-29°=61°,
tan∠ACE=$\frac{AE}{CE}$,
CE=$\frac{x}{1.8}$=$\frac{5x}{9}$,
由题意得,$\frac{10x}{7}$-$\frac{5x}{9}$=6,
解得x≈6.9.
答:渔船不改变航线继续向东航行,没有触礁的危险.
点评 本题考查了解直角三角形的应用,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
13.据统计,2015年我国高新技术产品出口总额约为40590亿元,40590亿这个数用科学记数法表示为( )
| A. | 4.0590×109 | B. | 0.40590×1010 | C. | 40.590×1011 | D. | 4.0590×1012 |
14.下列由左边到右边的变形,属于分解因式的变形是( )
| A. | ab+ac+d=a(b+c)+d | B. | a2-1=(a+1)(a-1) | C. | 12ab2c=3ab•4bc | D. | (a+1)(a-1)=a2-1 |
11.分别过一个三角形的3个顶点作对边的平行线,这些平行线两两相交,则构成的平行四边形的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列实数中,为无理数的是( )
| A. | $\sqrt{2}$ | B. | $\frac{1}{2}$ | C. | 0.2 | D. | -7 |
8.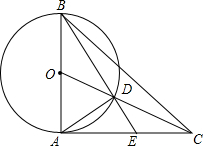 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )| A. | BD=$\frac{2}{3}$BC | B. | AD=OD | C. | AD=CD | D. | AE=CD |
12.已知方程x2+kx-6=0的一个根是x=2,则它的另一个根为( )
| A. | x=1 | B. | x=-2 | C. | x=3 | D. | x=-3 |
13.2015年6月国家主席习大大和比利时国王菲利普,在人民大会堂共同见证了两国公司在集成电路方面进行合作研发的签约仪式,两国将共同着力研发14纳米量产技术,这标志着我国芯片制造能力将进入国际顶尖水平.14纳米为0.000 000 014米,将0.000 000 014用科学记数法表示应为( )
| A. | 0.14×10-7 | B. | 1.4×10-8 | C. | 0.014×10-6 | D. | 14×10-9 |