题目内容
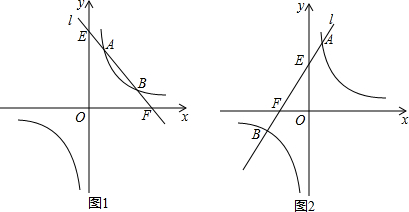
16.在四边形ABCD中,AB=AD,∠B=∠D=90°,∠BCD=120°,现将一个30°角的顶点落在点A处.(1)如图①,当该角的两边分别与BC、CD边相交于E、F时.求证:EF=BE+DF;
(2)现在将该角绕点A进行旋转,其两边分别与BC、CD边的延长线相交于点F,那么(1)中的结论是否仍然成立?若成立,说明理由;若不成立,试探究线段BE与DF之间的等量关系,并加以证明.(利用图②进行探索)

分析 (1)延长CB到H点,使BH=DF,连接AH,先证△ABH≌△ADF,再证△HAE≌△FAE即可解决问题;
(2)如图②,在BC上截取BH=DF,证得△ABH≌△ADF,然后证得△HAE≌△FAE,即可得到结论.
解答  解:(1)如图①,
解:(1)如图①,
延长CB到H点,使BH=DF,连接AH,
∵∠B=∠D=90°,∠BCD=120°,
∴∠D+∠B=180°,
∵∠ABE+∠ABH=180°,
∴∠ABH=∠D,
∵AD=AB,BH=DF,
∴在△ABH和△ADF中,
$\left\{\begin{array}{l}{BH=DF}\\{∠ABH=∠D}\\{AB=AD}\end{array}\right.$,
∴△ABH≌△ADF(SAS),
∴AH=AF,∠HAB=∠FAD,
∵∠DAB=60°,∠FAE=30°,
∴∠FAD+∠BAE=30°,
∴∠BAE+∠HAB=30°,即∠HAE=30°,
在△HAE和△EAF中,
$\left\{\begin{array}{l}{AH=AF}\\{∠HAE=∠EAF}\\{AE=AE}\end{array}\right.$,
∴△HAE≌△FAE(SAS),
∴HE=EF,
∵HE=HB+BE=DF+BE,
∴EF=BE+DF;
(2)(1)中的结论不成立 ,
,
如图②,在BC上截取BH=DF,
在△ABH与△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADF=90°}\\{BH=DF}\end{array}\right.$,
∴△ABH≌△ADF,
∴∠BAH=∠DAF,AH=AF,
∴∠EAF=30°,
∴∠BAH+∠EAD=30°,
∵∠B=∠D=90°,∠BCD=120°,
∴∠BAD=60°,
∴∠HAE=30°,
在△HAE与△FAE中,
$\left\{\begin{array}{l}{AH=AF}\\{∠HAE=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△HAE≌△FAE,
∴HE=EF,
∵BE=BH+HE,
∴BE=DF+EF.
点评 本题主要考查全等三角形的判定与性质,等腰三角形的性质,关键在于正确地作出辅助线,证明相关的三角形全等.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案| A. | (-11)2的算术平方根是±11 | |
| B. | 大于零而小于1的数的算术平方根比原数大 | |
| C. | 大于零而小于1的数的平方根比原数大 | |
| D. | 任何一个非负数的平方根都是非负数 |
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
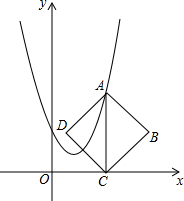 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )| A. | (2,2),(3,5) | B. | (2,2),(4,10) | C. | (3,5),(4,10) | D. | (2,2),(4,10),(6,26) |
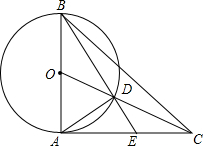 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )| A. | BD=$\frac{2}{3}$BC | B. | AD=OD | C. | AD=CD | D. | AE=CD |
| A. | 了解一批圆珠笔的寿命 | B. | 了解全国九年级学生身高的现状 | ||
| C. | 检查神舟号载人飞船的各零部件 | D. | 考察人们保护海洋的意识 |