题目内容
20.已知抛物线y1=ax2-4ax+3(a≠0)与y轴交于点A,A、B两点关于对称轴对称,直线OB分别与抛物线的对称轴相交于点C.(1)直接写出对称轴及B点的坐标;
(2)已知直线y2=bx-4b+3(b≠0)与抛物线的对称轴相交于点D.
①判断直线y2=bx-4b+3(b≠0)是否经过点B,并说明理由;
②若△BDC的面积为1,求b的值.
分析 (1)根据顶点公式即可求得对称轴,令x=0,求得A的坐标,然后根据轴对称的性质求得B的坐标;
(2)①把B的坐标代入即可判断;②求得OB的解析式,即可求得C的坐标,根据C的坐标和三角形的面积即可求得D的坐标,然后根据待定系数法即可求得.
解答 解:(1)∵抛物线为y1=ax2-4ax+3(a≠0),
∴对称轴是直线x=-$\frac{-4a}{2×a}$=2,
令x=0,则y=3,
∴A(0,3),
∵A、B两点关于对称轴对称,
∴B点的坐标为(4,3);
(2)①经过,
理由:把x=4代入直线y2=bx-4b+3(b≠0)点y2=3,
故直线y2=bx-4b+3(b≠0)是否经过点B;
②∵B(4,3),
∴直线OB为:y=$\frac{3}{4}$x,
把x=2代入得y=$\frac{3}{2}$,
∴C(2,$\frac{3}{2}$),
∵△BDC的面积为1,
∴$\frac{1}{2}$CD•(4-2)=1,
∴CD=1,
∴D(2,$\frac{5}{2}$)或(2,$\frac{1}{2}$),
把(2,$\frac{5}{2}$)代入y2=bx-4b+3得$\frac{5}{2}$=2b-4b+3,
解得b=$\frac{1}{4}$;
把(2,$\frac{1}{2}$)代入y2=bx-4b+3得$\frac{1}{2}$=2b-4b+3,
解得b=$\frac{5}{4}$,
∴b的值为$\frac{1}{4}$或$\frac{5}{4}$.
点评 本题考查了二次函数的性质,轴对称的性质,二次函数图象上点的坐标特征以及三角形面积等,根据待定系数法求得直线的解析式,进而求得C和D的坐标是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.分别过一个三角形的3个顶点作对边的平行线,这些平行线两两相交,则构成的平行四边形的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.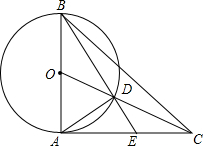 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
 如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )
如图,在△ABC中,AB=AC,O是线段AB的中点,线段OC与以AB为直径的⊙O交于点D,射线BD交AC于点E,∠BAC=90°,那么下列等式成立的是( )| A. | BD=$\frac{2}{3}$BC | B. | AD=OD | C. | AD=CD | D. | AE=CD |
12.已知方程x2+kx-6=0的一个根是x=2,则它的另一个根为( )
| A. | x=1 | B. | x=-2 | C. | x=3 | D. | x=-3 |
9. 如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )
如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )
 如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )
如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
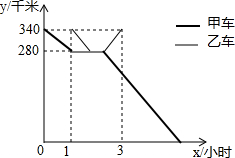 已知重庆和成都相距340千米,甲车早上八点从重庆出发往成都运送物资,行驶1小时后,汽车突然出现故障,立即通知技术人员乘乙车从重庆赶来维修(通知时间不计),乙车达到后经30分钟修好甲车,然后以原速返回重庆,同时甲车以原来速度的1.5倍继续前往成都.两车分别距离成都的路程y(千米)与甲车所用时间x(小时)之间的函数图象如图所示,下列四个结论:①甲车提速后的速度是90千米/时;②乙车的速度是70千米/时;③甲车修好的时间为10点15分;④甲车达到成都的时间为13点15分,其中,正确的结论是①③(填序号)
已知重庆和成都相距340千米,甲车早上八点从重庆出发往成都运送物资,行驶1小时后,汽车突然出现故障,立即通知技术人员乘乙车从重庆赶来维修(通知时间不计),乙车达到后经30分钟修好甲车,然后以原速返回重庆,同时甲车以原来速度的1.5倍继续前往成都.两车分别距离成都的路程y(千米)与甲车所用时间x(小时)之间的函数图象如图所示,下列四个结论:①甲车提速后的速度是90千米/时;②乙车的速度是70千米/时;③甲车修好的时间为10点15分;④甲车达到成都的时间为13点15分,其中,正确的结论是①③(填序号)