题目内容
19.计算:(1)(-1)2012+(-$\frac{1}{2}$)-2-(3.14-π)0;
(2)(-x2)3•x2+(2x2)4-3(-x)3•x5
(3)(x-y+1)(x+y-1)
(4)1.2342+0.7662+2.468×0.766.
分析 (1)原式利用乘方的意义,零指数幂、负整数指数幂法则计算即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;
(3)原式利用平方差公式及完全平方公式化简即可得到结果;
(4)原式利用完全平方公式计算即可得到结果.
解答 解:(1)原式=1+4-1=4;
(2)原式=-x8+16x8+3x8=18x8;
(3)原式=x2-(y-1)2=x2-y2+2y-1;
(4)原式=(1.234+0.766)2=4.
点评 此题考查了整式的混合运算,零指数幂、负整数指数幂,熟练掌握运算法则及公式是解本题的关键.

练习册系列答案
相关题目
9.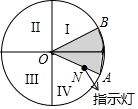 如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
 如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{7}{12}$ | C. | $\frac{5}{12}$ | D. | $\frac{5}{9}$ |
14.方程(x-2)(x-4)=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 8或10 |
11.下列运算正确的是( )
| A. | an•a2=a2n | B. | a3•a2=a6 | C. | an•(a2)n=a2n+2 | D. | a2n-3÷a-3=a2n |
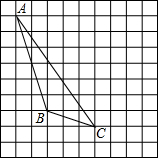 如图,在方格纸内将△ABC水平向右平移4个单位,再向下后平移1得到△A′B′C′.
如图,在方格纸内将△ABC水平向右平移4个单位,再向下后平移1得到△A′B′C′.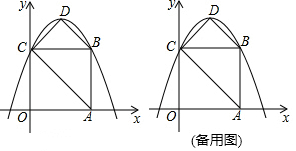
 如图,?ABCD的对角线AC和BD相交于点O,那么图中的全等三角形共有4对.
如图,?ABCD的对角线AC和BD相交于点O,那么图中的全等三角形共有4对.