Question

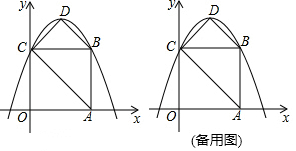
8．如图，在平面直角坐标系中，正方形OABC的边长为4，顶点A，C分别在x轴、y轴的正半轴．抛物线y=-$\frac{1}{2}$x²+bx+c经过B，C两点，点D为抛物线的顶点，连接AC，BD，CD．
（1）求此抛物线的解析式；
（2）求此抛物线顶点D的坐标和四边形ABDC的面积．

Answer 1

分析 （1）由正方形的性质可求得B、C的坐标，代入抛物线解析式可求得b、c的值，则可求得抛物线的解析式；
（2）把抛物线解析式化为顶点式可求得D点坐标，再由S_{四边形ABDC}=S_△ABC+S_△BCD可求得四边形ABDC的面积．

解答 解：
（1）∵正方形OABC的边长为4，
∴OC=BC=AB=OA=4，
∴C（0，4），B（4，4），
∵抛物线y=-$\frac{1}{2}$x²+bx+c经过B，C两点，
∴$\left\{\begin{array}{l}{c=4}\\{-8+4b+c=4}\end{array}\right.$，解得$\left\{\begin{array}{l}{b=2}\\{c=4}\end{array}\right.$，
∴抛物线解析式为y=-$\frac{1}{2}$x²+2x+4；
（2）∵y=-$\frac{1}{2}$x²+2x+4=-$\frac{1}{2}$（x-2）²+6，
∴D（2，6），
∴D到BC的距离为6-4=2，
∴S_{四边形ABDC}=S_△ABC+S_△BCD=$\frac{1}{2}$×4×4+$\frac{1}{2}$×4×2=12．

点评 本题为二次函数的综合应用，涉及正方形的性质、待定系数法、二次函数的性质、三角形的面积等知识．在（1）中确定出B、C的坐标是解题的关键，在（2）中把四边形转化成两个三角形是解题的关键．本题考查知识点较多，综合性较强，但难度不大．