Question

4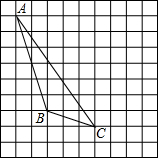．如图，在方格纸内将△ABC水平向右平移4个单位，再向下后平移1得到△A′B′C′．
（1）画出平移后的△A′B′C′；
（2）画出AB边上的高线CD（利用三角板画图）；
（3）画出△ABC中AB边上的中线CE；
（4）图中AC与A′C′的关系是：平行且相等；
（5）△BCE的面积为4．
（6）若△A″BC的面积与△ABC面积相同，则A″（A″在格点上）的位置（除A点外）共有3个．

Answer 1

分析 （1）分别作出点A、B、C向右平移4个单位，再向下后平移1得到的对应点，顺次连接即可得；
（2）根据三角形高的定义作出线段可得；
（3）根据三角形中线的定义作出线段可得；
（4）根据平移的性质即可得；
（5）利用割补法求解可得；
（6）根据两三角形的底边公共，而面积相等知点A″应位于过点A且平行于BC的直线上，据此可得．

解答 解：（1）如图，△A′B′C′即为所求；

（2）如图，线段CD即为所求；
（3）如图，线段CE即为所求；
（4）图中AC与A′C′平行且相等，
故答案为：平行且相等；
（5）S_△BCE=$\frac{1}{2}$×4×4-$\frac{1}{2}$×1×3-1×1-$\frac{1}{2}$×1×3=4；
（6）若△A″BC的面积与△ABC面积相同，
则点A″应位于过点A且平行于BC的直线上，由图可知，这样的格点A″共有3个，
故答案为：3．

点评 本题主要考查平移变换，熟练掌握平移的定义和性质及割补法求三角形的面积、共底等高的两三角形的面积问题是解题的关键．