题目内容
9. 如图,?ABCD的对角线AC和BD相交于点O,那么图中的全等三角形共有4对.
如图,?ABCD的对角线AC和BD相交于点O,那么图中的全等三角形共有4对.
分析 根据平行四边形的性质及全等三角形的判定方法进行分析,从而得到答案.
解答 解:∵ABCD是平行四边形
∴AD=BC,AB=CD,AO=CO,BO=DO,
在△ABO和△CDO中,$\left\{\begin{array}{l}{OA=OC}&{\;}\\{∠AOB=∠COD}&{\;}\\{OB=OD}&{\;}\end{array}\right.$,
∴△ABO≌△CDO(SAS),
同理:△ADO≌△CBO;
在△ABD和△CDB中,$\left\{\begin{array}{l}{AB=CD}&{\;}\\{AD=CB}&{\;}\\{BD=DB}&{\;}\end{array}\right.$,
∴△ABD≌△CDB(SSS),
同理:△ACD≌△CAB;
∴图中的全等三角形共有4对.
故答案为:4.
点评 本题主要考查了平行四边形的性质、全等三角形的判定;熟记平行四边形的性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17. 如图,在△ABC中,∠ACB=90°,分别以点A,B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点M,N,作直线MN分别交AB,AC于点D,E,连结CD,BE,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A,B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点M,N,作直线MN分别交AB,AC于点D,E,连结CD,BE,下列结论错误的是( )
 如图,在△ABC中,∠ACB=90°,分别以点A,B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点M,N,作直线MN分别交AB,AC于点D,E,连结CD,BE,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A,B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点M,N,作直线MN分别交AB,AC于点D,E,连结CD,BE,下列结论错误的是( )| A. | AD=CD | B. | BE>CD | C. | ∠BEC=∠BDC | D. | BE平分∠CBD |
14. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )| A. | abc<0 | B. | 4a-2b+c>0 | C. | b2-4ac<0 | D. | a+b+c<0 |
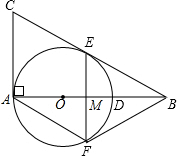 如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边AB相交于点D,与边BC相切于点E.
如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边AB相交于点D,与边BC相切于点E.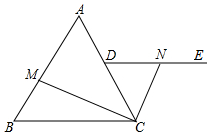 如图,在边长为6的等边△ABC中,D为AC中点,射线DE∥BC,M,N分别为线段AB与射线DE上的点,连结CM,CN,若BM=DN,则CM+CN的最小值为3$\sqrt{7}$.
如图,在边长为6的等边△ABC中,D为AC中点,射线DE∥BC,M,N分别为线段AB与射线DE上的点,连结CM,CN,若BM=DN,则CM+CN的最小值为3$\sqrt{7}$. 如图,在正方形ABCD中,对角线AC,BD交于点O,现有一块足够大的直角三角板的直角顶点与点O重合,当直角三角板绕着点O旋转时,两条直角边OP、OQ分别保持与边AB、边BC相交于点E、F,连结EF,下列结论:①EF=OB,②EF=$\sqrt{2}$OF;③当EF∥AC时,△BEF的周长最小;④当BE变化时,四边形OEBF的面积也随之变化.其中结论正确的个数为( )
如图,在正方形ABCD中,对角线AC,BD交于点O,现有一块足够大的直角三角板的直角顶点与点O重合,当直角三角板绕着点O旋转时,两条直角边OP、OQ分别保持与边AB、边BC相交于点E、F,连结EF,下列结论:①EF=OB,②EF=$\sqrt{2}$OF;③当EF∥AC时,△BEF的周长最小;④当BE变化时,四边形OEBF的面积也随之变化.其中结论正确的个数为( )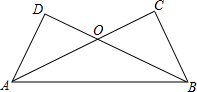 如图,已知OC=OD,∠OAB=∠OBA,求证:AD=BC.
如图,已知OC=OD,∠OAB=∠OBA,求证:AD=BC.