题目内容
9.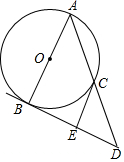 如图,在Rt△ABC中,BC=2cm,AC=4cm,以AB长为直径作圆⊙O,过点B的切线与AC的延长线交于点D,E是BD的中点,连接CE.
如图,在Rt△ABC中,BC=2cm,AC=4cm,以AB长为直径作圆⊙O,过点B的切线与AC的延长线交于点D,E是BD的中点,连接CE.求证:CE是⊙O的切线.
分析 连接OC,由AB为⊙O的直径知∠ACB=∠BCD=90°,从而在Rt△ABC和Rt△BCD中,根据OA=OB=OC、BE=DE知∠1=∠2、∠3=∠4,最后由BD是⊙O的切线,即∠2+∠4=90°可得∠1+∠3=90°,即可得证.
解答 证明:如图,连接OC,
∵AB为⊙O的直径,
∴∠ACB=∠BCD=90°,
在Rt△ABC和Rt△BCD中,
∵OA=OB=OC、BE=DE,
∴∠1=∠2,∠3=∠4,
∵BD是⊙O的切线,
∴∠2+∠4=90°,
∴∠1+∠3=90°,
∴CE是⊙O的切线.
点评 本题主要考查切线的判定与性质、圆周角定理及直角三角形的性质,熟练掌握切线的判定是关键:连接半径,证明半径与直线垂直.

练习册系列答案
相关题目
3.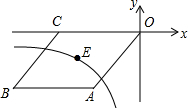 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )
 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
19. 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )
 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )| A. | (2017,0) | B. | (2017,$\sqrt{3}$) | C. | (2017,-$\sqrt{3}$) | D. | (2016,0) |
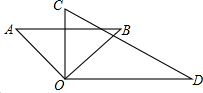 如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=$\frac{2}{3}$∠AOD,则∠AOD=108°.
如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=$\frac{2}{3}$∠AOD,则∠AOD=108°.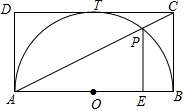 如图,在矩形ABCD中,以边AB为直径的半圆O恰与对边CD相切于T,与对角线AC交于P,PE⊥AB于E,AB=10,则PE的长为4cm.
如图,在矩形ABCD中,以边AB为直径的半圆O恰与对边CD相切于T,与对角线AC交于P,PE⊥AB于E,AB=10,则PE的长为4cm. 一个几何体的主视图和俯视图如图所示,那么它的左视图可能是( )
一个几何体的主视图和俯视图如图所示,那么它的左视图可能是( )



 某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:
某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答: 如图,△ABC内接于⊙O,直径AB=8,D为BA延长线上一点且AD=4,E为线段CD上一点,满足∠EAC=∠BAC,则AE=2.
如图,△ABC内接于⊙O,直径AB=8,D为BA延长线上一点且AD=4,E为线段CD上一点,满足∠EAC=∠BAC,则AE=2.