题目内容
1．
某生物兴趣小组在四天的实验研究中发现：骆驼的体温会随外部环境温度的变化而变化，而且在这四天中每昼夜的体温变化情况相同，他们将一头骆驼前两昼夜的体温变化情况绘制成右图，请根据图象回答：（1）在这个问题中，自变量是什么？因变量是什么？
（2）第一天中，在什么时间范围内这头骆驼的体温是上升的？它的体温从最低上升到最高需要多少时间？
（3）第三天12时这头骆驼的体温是多少？
分析 （1）根据题意即可得到结论；
（2）根据函数图象找出0～24小时图象随时间增大而增大的部分即可，然后求出从体温开始上升到上升结束的时间差即可；
（3）根据函数图象找出12时对应的体温值即可．
解答 解：（1）在这个问题中，自变量是外部环境温度；因变量是骆驼的体温；
（2）由图可知，第一天中，从4时到16时这头骆驼的体温是上升的，
它的体温从最低上升到最高需要16-4=12小时；
（3）第三天12时这头骆驼的体温是39℃．
点评 本题考查利用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，准确识图是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
15．若顺次连接一个四边形的各边的中点所得的四边形是矩形，则原来的四边形的两条对角线（ ）
| A． | 互相垂直且相等 | B． | 相等 | C． | 互相平分且相等 | D． | 互相垂直 |
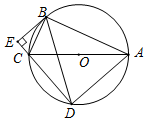如图，⊙O是△ABC的外接圆，AC为直径，弦ED=BA，BE⊥DC交DC的延长线于点E，求证：
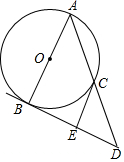如图，在Rt△ABC中，BC=2cm，AC=4cm，以AB长为直径作圆⊙O，过点B的切线与AC的延长线交于点D，E是BD的中点，连接CE．
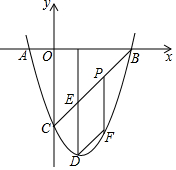如图，抛物线y=x2+bx+c与x轴相交于A、B两点，点B的坐标为（3，0），与y轴相交于点C（0，-3），顶点为D．
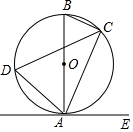如图，已知AB是⊙O的直径，点C，D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．
10．
如图，在平面直角坐标系中，∠AOB=30°，点A的坐标为（2，0），过点A作AA1⊥OB，垂足为点A1，过A1作A1A2⊥x轴，垂足为点A2；再过点A2作A2A3⊥OB，垂足为点A3；再过点A3作A3A4⊥x轴，垂足为点A4…；这样一直作下去，则A2017的横坐标为（ ）
如图，在平面直角坐标系中，∠AOB=30°，点A的坐标为（2，0），过点A作AA1⊥OB，垂足为点A1，过A1作A1A2⊥x轴，垂足为点A2；再过点A2作A2A3⊥OB，垂足为点A3；再过点A3作A3A4⊥x轴，垂足为点A4…；这样一直作下去，则A2017的横坐标为（ ）| A． | $\frac{3}{2}$•（$\frac{\sqrt{3}}{2}$）2015 | B． | $\frac{3}{2}$•（$\frac{\sqrt{3}}{2}$）2016 | C． | $\frac{3}{2}$•（$\frac{\sqrt{3}}{2}$）2017 | D． | $\frac{3}{2}$•（$\frac{\sqrt{3}}{2}$）2018 |
11．
如图，双曲线y=$\frac{6}{x}$（x＞0）经过线段AB的中点M，则△AOB的面积为（ ）
如图，双曲线y=$\frac{6}{x}$（x＞0）经过线段AB的中点M，则△AOB的面积为（ ）| A． | 18 | B． | 24 | C． | 6 | D． | 12 |