题目内容
3.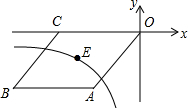 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 根据勾股定理得到OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,根据菱形的性质得到AB=OA=5,AB∥x轴,求得B(-8,-4),得到E(-4,-2),于是得到结论.
解答 解:∵点A的坐标为(-3,-4),
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵四边形AOCB是菱形,
∴AB=OA=5,AB∥x轴,
∴B(-8,-4),
∵点E是菱形AOCB的中心,
∴E(-4,-2),
∴k=-4×(-2)=8,
故选B.
点评 本题考查了反比例函数图象上点的坐标特征,菱形的性质,勾股定理,正确的识别图形是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
11.四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
| A. | AB=DC,∠ABC=∠ADC | B. | AD∥BC,AB∥DC | C. | AB=DC,AD=BC | D. | OA=OC,OB=OD |
18.若矩形的长和宽是方程x2-7x+12=0的两根,则矩形的对角线之和为( )
| A. | 5 | B. | 7 | C. | 8 | D. | 10 |
15.若顺次连接一个四边形的各边的中点所得的四边形是矩形,则原来的四边形的两条对角线( )
| A. | 互相垂直且相等 | B. | 相等 | C. | 互相平分且相等 | D. | 互相垂直 |
 如图,在直角坐标系中,△ABC的三个顶点均在格点上,其位置如图所示.现将△ABC沿AA′的方向平移,使得点A移至图中的点A′的位置,写出平移过程中线段AB扫过的面积8.
如图,在直角坐标系中,△ABC的三个顶点均在格点上,其位置如图所示.现将△ABC沿AA′的方向平移,使得点A移至图中的点A′的位置,写出平移过程中线段AB扫过的面积8.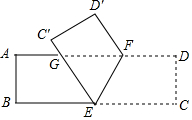 如图,将一张长方形纸片ABCD沿EF折叠,使顶点C、D分别落在C′、D′处,C′E交AF于点G,若∠CEF=65°,则∠GFD′=50°.
如图,将一张长方形纸片ABCD沿EF折叠,使顶点C、D分别落在C′、D′处,C′E交AF于点G,若∠CEF=65°,则∠GFD′=50°.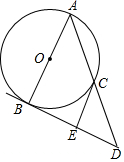 如图,在Rt△ABC中,BC=2cm,AC=4cm,以AB长为直径作圆⊙O,过点B的切线与AC的延长线交于点D,E是BD的中点,连接CE.
如图,在Rt△ABC中,BC=2cm,AC=4cm,以AB长为直径作圆⊙O,过点B的切线与AC的延长线交于点D,E是BD的中点,连接CE.