题目内容
19.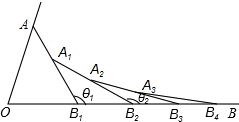 如图所示,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连结A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连结A2B2…按此规律下去,记∠A2B1 B2=θ1,∠A3B2B3=θ2,…,∠An+1Bn Bn+1=θn,则θ2016-θ2015的值为( )
如图所示,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连结A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连结A2B2…按此规律下去,记∠A2B1 B2=θ1,∠A3B2B3=θ2,…,∠An+1Bn Bn+1=θn,则θ2016-θ2015的值为( )| A. | $\frac{180°+α}{{2}^{2015}}$ | B. | $\frac{180°-α}{{2}^{2015}}$ | C. | $\frac{180°+α}{{2}^{2016}}$ | D. | $\frac{180°-α}{{2}^{2016}}$ |
分析 根据等腰三角形两底角相等用α表示出∠A1B1O,再根据平角等于180°列式用α表示出θ1,再用θ1表示出θ2,并求出θ2-θ1,依此类推求出θ3-θ2,…,θ2013-θ2012,即可得解.
解答  解:∵OA1=OB1,∠AOB=α,
解:∵OA1=OB1,∠AOB=α,
∴∠A1B1O=$\frac{1}{2}$(180°-α),
∴$\frac{1}{2}$(180°-α)+θ1=180,
整理得,θ1=$\frac{180°+a}{2}$,
∵B1B2=B1A2,∠A2B1B2=θ1,
∴∠A2B2B1=$\frac{1}{2}$(180°-θ1),
∴$\frac{1}{2}$(180°-θ1)+θ2=180°,
整理得θ2=$\frac{180°+{θ}_{1}}{2}$=$\frac{3×180°+a}{4}$,
∴θ2-θ1=$\frac{3×180°+a}{4}$-$\frac{180°+a}{2}$=$\frac{180°-a}{4}$=$\frac{180°-a}{{2}^{2}}$,
同理可求θ3=$\frac{180°+{θ}_{2}}{2}$=$\frac{7×180°+a}{8}$,
∴θ3-θ2=$\frac{7×180°+a}{8}$-$\frac{3×180°+a}{4}$=$\frac{180°-a}{8}$=$\frac{180°-a}{{2}^{3}}$,
…,
依此类推,θ2016-θ2015=$\frac{180°-a}{{2}^{2016}}$.
故选D.
点评 本题考查了等腰三角形两底角相等的性质,图形的变化规律,依次求出相邻的两个角的差,得到分母成2的指数次幂变化,分子不变的规律是解题的关键.

练习册系列答案
相关题目
7.在数轴上表示-5的点离开原点的距离等于( )
| A. | 5 | B. | -5 | C. | ±5 | D. | 10 |
11.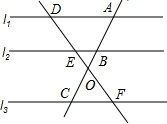 如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
 如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AB}{BO}$=$\frac{DE}{EO}$ | C. | $\frac{OB}{OC}$=$\frac{OE}{OF}$ | D. | $\frac{AD}{CF}$=$\frac{AO}{AC}$ |
8.若多项式x2-ax-1可分解为(x+b)(x-2),则a+b的值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
 如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D.试说明:DE=DB.
如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D.试说明:DE=DB.