题目内容
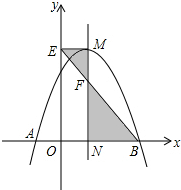 如图,抛物线y=-x2+2x+3与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.
如图,抛物线y=-x2+2x+3与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.(1)求F的坐标.
(2)求△EMF与△BNF的面积之和.
考点:二次函数图象上点的坐标特征,待定系数法求一次函数解析式,三角形的面积
专题:计算题
分析:(1)先把解析式配成顶点式得到顶点M的坐标是(1,4),对称轴是直线x=1,则点E的坐标是(0,4),再求出B(3,0),然后利用待定系数法求出直线BE的解析式为y=-
x+4,再计算x=1时所对应的一次函数值即可确定F点坐标;
(2)先计算出EM=1,MF=4-
=
,FN=
,BN=3-1=2,然后根据三角形面积公式求解.
| 4 |
| 3 |
(2)先计算出EM=1,MF=4-
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
解答:解:(1)∵y=-x2+2x+3=-(x-1)2+4,
∴顶点M的坐标是(1,4),对称轴是直线x=1,
∵ME⊥y轴,
∴点E的坐标是(0,4),
解方程-x2+2x+3=0得x1=-1,x2=3,
∴A(-1,0),B(3,0),
设直线BE的解析式为y=kx+b,
把B(3,0),E(0,4)代入得
,解得
,
∴直线BE的解析式为y=-
x+4,
∵当x=1时,y=-
x+4=
,
∴所以F的坐标是(1,
);
(2)由(1)可得EM=1,MF=4-
=
,FN=
,BN=3-1=2,
S△EFM+S△BNF=
•1•
+
•2•
=
.
∴顶点M的坐标是(1,4),对称轴是直线x=1,
∵ME⊥y轴,
∴点E的坐标是(0,4),
解方程-x2+2x+3=0得x1=-1,x2=3,
∴A(-1,0),B(3,0),
设直线BE的解析式为y=kx+b,
把B(3,0),E(0,4)代入得
|
|
∴直线BE的解析式为y=-
| 4 |
| 3 |
∵当x=1时,y=-
| 4 |
| 3 |
| 8 |
| 3 |
∴所以F的坐标是(1,
| 8 |
| 3 |
(2)由(1)可得EM=1,MF=4-
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
S△EFM+S△BNF=
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
| 10 |
| 3 |
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了待定系数法求一次函数解析式.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
一筐苹果4千克,增加
后,列出的算式为( )
| 1 |
| 2 |
A、4+
| ||
B、4×(1+
| ||
| C、4÷(1+) | ||
D、4×(1-
|
 如图,∠1=∠2,∠3=∠4,∠A=80°,求∠BOC的度数.
如图,∠1=∠2,∠3=∠4,∠A=80°,求∠BOC的度数.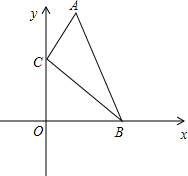 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.