题目内容
已知抛物线y=ax2+bx+c与x轴的交点是A(-1,0),B(3,0),与y轴的交点是C,顶点是D.若四边形ABDC的面积是18,求抛物线所对应的函数解析式.
考点:待定系数法求二次函数解析式
专题:
分析:设二次函数解析式为y=ax2+bx+c,把A、B坐标代入可用a表示出b、c,可表示出C、D的坐标,再利用面积为18,可求得a的值,
解答: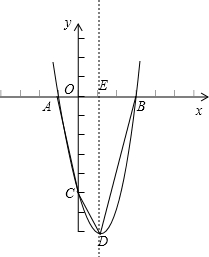 解:设二次函数解析式为y=ax2+bx+c,
解:设二次函数解析式为y=ax2+bx+c,
∵抛物线与x两交点为A(-1,0),B(3,0),
∴a-b+c=0,9a+3b+c=0
∴b=-2a,c=-3a,
∴D的坐标为(1,-4a),C坐标为(0,-3a)
当a>0时,如图,设对称轴交x轴于点E,
则S四边形ABCD=S△AOC+S△BED+S梯形OCDE,
又S△AOC=
AO•OC,S△BED=
BE•DE,S梯形OCDE=
(OC+OD)•OE,
即18=
×1×3a+
×2×4a+
×(3a+4a)×1,
∴a=2,
∴抛物线解析式为:y=2x2-4x-6,
同理可解,当a<0时抛物线为:y=-2x2+4x+6,
综上可知抛物线的解析式为y=2x2-4x-6或y=-2x2+4x+6.
 解:设二次函数解析式为y=ax2+bx+c,
解:设二次函数解析式为y=ax2+bx+c,∵抛物线与x两交点为A(-1,0),B(3,0),
∴a-b+c=0,9a+3b+c=0
∴b=-2a,c=-3a,
∴D的坐标为(1,-4a),C坐标为(0,-3a)
当a>0时,如图,设对称轴交x轴于点E,
则S四边形ABCD=S△AOC+S△BED+S梯形OCDE,
又S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即18=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a=2,
∴抛物线解析式为:y=2x2-4x-6,
同理可解,当a<0时抛物线为:y=-2x2+4x+6,
综上可知抛物线的解析式为y=2x2-4x-6或y=-2x2+4x+6.
点评:本题主要考查待定系数法求二次函数解析式,把四边形ABCD的面积用a表示出来是解题的关键,注意分类讨论.

练习册系列答案
相关题目
 表示a-b-c,图
表示a-b-c,图 表示x+z-y-w,则
表示x+z-y-w,则 +
+ =
=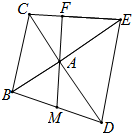 如图,△ABC、△DAE都是等腰直角三角形,M为BD中点,M、A、F共线,求证:①AF⊥CE;②CE=2DM.
如图,△ABC、△DAE都是等腰直角三角形,M为BD中点,M、A、F共线,求证:①AF⊥CE;②CE=2DM. 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=8cm,求点B到地面的距离.
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=8cm,求点B到地面的距离.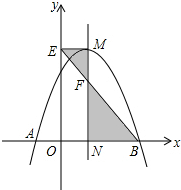 如图,抛物线y=-x2+2x+3与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.
如图,抛物线y=-x2+2x+3与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.