题目内容
3.对数概念:如果ab=N(a>0,a≠1),那么幂指数b叫做以a为底数N的对数,记作b=logaN.如23=8,则有log28=3.(1)计算:log21=0;log3$\frac{1}{3}$=-1;
(2)用对数的概念证明,其中M,N,n都是正数,a>0,a≠1,b>0,b≠1:
①loga(M•N)=logaM+logaN ②loga$\frac{M}{N}$=logaM-logaN
③logaMn=nlogaM ④logab=$\frac{1}{lo{g}_{b}a}$
(以上四个结论只需从中选出一个证明即可.)
(3)用(2)的结论计算:
[(1-log63)2+log62•log618]÷log64.
分析 (1)根据对数的定义求出即可;
(2)设:logaM=x,logaN=y,根据对数定义可知:ax=M,ay=N,ax•ay=M•N求出ax+y=M•N,根据对数的定义求出即可;
(3)根据对数的性质对代数式逐步进行化简即可.
解答 解:(1)log21=0,log3$\frac{1}{3}$=-1,
故答案为:0,-1;
(2)①
证明:设:logaM=x,logaN=y,
∵根据对数定义可知:ax=M,ay=N,
∴ax•ay=M•N,
∴ax+y=M•N,
即loga(M•N)=x+y=logaM+logaN;
(3)[(1-log63)2+log62•log618]÷log64
=[log26(log62+log6÷2log62
=(log66+1)÷2
=1.
点评 本题考查了对对数的定义和性质的应用,能根据定义和性质进行变形是解此题的关键,是一道基础题目.

练习册系列答案
相关题目
8.某学校组织学生到距离学校6千米的科技馆去参观,小华因事没能乘上学校的包车,于是准备在学校门口改乘出租车去科技馆,出租车标注收费有两种类型,如表:
(1)设出租车行驶的里程为x千米(x≥3且x取正整数),分别写出两种类型的总收费y(用含x的代数式表示);
(2)小华身上仅有10元,他乘出租车到科技馆车费够不够?请说明理由.
| 里程 | 甲类收费(元) | 乙类收费(元) |
| 3千米以下(包含3千米) | 5.00 | 6.00 |
| 3千米以上,每增加1千米 | 1.60 | 1.30 |
(2)小华身上仅有10元,他乘出租车到科技馆车费够不够?请说明理由.
15.反比例函数y=$\frac{k}{x}$(k<0),下列说法正确的是( )
| A. | 可以取任意实数 | B. | 函数图象在第一、三象限 | ||
| C. | 图象过点(1,k)和(-k,-1) | D. | 与函数y=4x的图象有两个交点 |
 如图,在△ABC中,∠C>∠B,AD是△ABC的角平分线,AE⊥BC于点E,试说明∠DAE=$\frac{1}{2}$(∠C-∠B).
如图,在△ABC中,∠C>∠B,AD是△ABC的角平分线,AE⊥BC于点E,试说明∠DAE=$\frac{1}{2}$(∠C-∠B).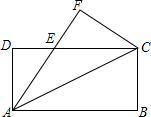 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E 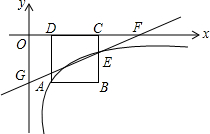 如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0).
如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0).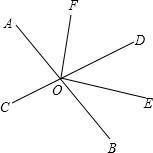 如图,两条直线AB,CD相交于点O,OE平分∠BOD.
如图,两条直线AB,CD相交于点O,OE平分∠BOD.