题目内容
17．
如图，在△ABC中，∠C＞∠B，AD是△ABC的角平分线，AE⊥BC于点E，试说明∠DAE=$\frac{1}{2}$（∠C-∠B）．
分析 根据直角三角形两锐角互余得出∠CAE+∠C=90°，再根据角平分线定义得出∠CAD=∠BAD，然后根据∠DAE=∠CAD-∠CAE进行计算即可得解．
解答 解：∵AE⊥BC，
∴∠CAE=90°-∠C，
∵AD是△ABC的角平分线，
∴∠CAD=$\frac{1}{2}$∠BAC，
∴∠DAE=∠CAD-∠CAE=$\frac{1}{2}$∠BAC-（90°-∠C）=$\frac{1}{2}（180°-∠B-∠C）$-90°+∠C=$\frac{1}{2}$（∠C-∠B）．
点评 本题考查了三角形的内角和定理，三角形的角平分线，高线的定义，准确识图，找出各角度之间的关系是解题的关键．
练习册系列答案
相关题目
7．
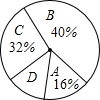某市为了了解七年级学生的身体素质情况，随机抽取了本市七年级部分学生的身体素质测试成绩为样本，按A（优秀）、B（良好）、C（合格）、D（不合格）四个等级进行统计，并将统计结果绘制成如图的统计图表，请你结合图表所给的信息解答下列问题：
（1）请你根据图表中的信息计算出所抽取的样本容量为500；
（2）请将表格中缺少的数据补充完整；
（3）如果本市共有50000名七年级学生，试估计出合格以上（包括合格）的学生有44000人．
某市为了了解七年级学生的身体素质情况，随机抽取了本市七年级部分学生的身体素质测试成绩为样本，按A（优秀）、B（良好）、C（合格）、D（不合格）四个等级进行统计，并将统计结果绘制成如图的统计图表，请你结合图表所给的信息解答下列问题：| 等级 | A（优秀） | B（良好） | C（合格） | D（不及格） |
| 人数 | 80 | 200 | 160 | 60 |
（2）请将表格中缺少的数据补充完整；
（3）如果本市共有50000名七年级学生，试估计出合格以上（包括合格）的学生有44000人．
平行四边形中，E、F分别是BC、CD边上的中点，那么与阴影部分面积相等的三角形有8个．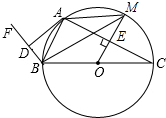
如图，已知BC为⊙O的直径，BA平分∠FBC交⊙O于点A，D是射线BF上的一点，且满足$\frac{BD}{BA}$=$\frac{BA}{BC}$，过点O作OM⊥AC于点E，交⊙O于点M，连接BM，AM．
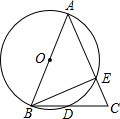如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°，给出以下五个结论：①∠EBC=22.5°；②BD=DC；③AE=2EC；④劣弧$\widehat{AE}$是劣弧$\widehat{BD}$的2倍；⑤AE=BC，其中正确的序号是①②④．
2．在反比例函数y=$\frac{9}{x}$的图象上，到x轴和y轴的距离相等的点有（ ）
| A． | 1个 | B． | 2个 | C． | 4个 | D． | 无数个 |