题目内容
14.先化简,再求值:$\frac{{{x^2}-2x}}{x+2}$÷$\frac{x}{x+2}$,其中x=-3.分析 利用分解因式和消元等方法将原分式化简成x-2,并找出x的取值范围,再将x=-3代入化简后的整式中即可得出结论.
解答 解:原式=$\frac{x(x-2)}{x+2}$•$\frac{x+2}{x}$=x-2.
∵(x+2)x≠0,
∴x≠-2且x≠0,
当x=-3时,
原式=x-2=-3-2=-5.
点评 本题考查了分式的化简求值,解题的关键是将原分式化简成x-2.本题属于基础题,难度不大,解决该题型题目时,先对原分式进行化简,再将给定的数值代入化简后的分式(或整式)中求出结果即可.

练习册系列答案
相关题目
5.已知:(a-b)2=9;(a+b)2=25,则a2+b2=( )
| A. | 34 | B. | 16 | C. | -16 | D. | 17 |
3.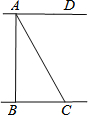 如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.
如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.
 如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.
如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.| A. | $\frac{45}{cos50°}$ | B. | 45•cos50° | C. | $\frac{45}{tan50°}$ | D. | 45•tan50° |
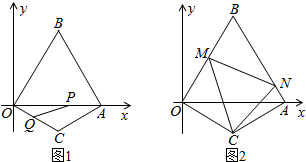 已知:如图(1),△OAB是边长为2的等边三角形,0A在x轴上,点B在第一象限内;△OCA是一个等腰三角形,OC=AC,顶点C在第四象限,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
已知:如图(1),△OAB是边长为2的等边三角形,0A在x轴上,点B在第一象限内;△OCA是一个等腰三角形,OC=AC,顶点C在第四象限,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
 实数a、b在数轴上的位置如图所示,则化简 $\sqrt{{{(-a)}^2}}+\sqrt{b^2}-\sqrt{{{(a+b)}^2}}$的结果为2b.
实数a、b在数轴上的位置如图所示,则化简 $\sqrt{{{(-a)}^2}}+\sqrt{b^2}-\sqrt{{{(a+b)}^2}}$的结果为2b.