题目内容
如图1,在△ABC中,∠CBE为△ABC的一个外角,AP,BP分别平分∠BAC和∠CBE,且交于点P,若∠BPA=40°,

(1)求∠ACB的度数;
(2)如图2,连CP,求∠BCP的度数.

(1)求∠ACB的度数;
(2)如图2,连CP,求∠BCP的度数.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)如图(1)设∠BA=2α,∠ACB=2β;证明∠EBP=∠BPA+α,∠EBP=
(2α+2β),得到∠BPA+α=α+β,故β=∠BPA=40°,即可解决问题.
(2)如图,作辅助线;证明PC平分∠BCM,即可解决问题.
| 1 |
| 2 |
(2)如图,作辅助线;证明PC平分∠BCM,即可解决问题.
解答: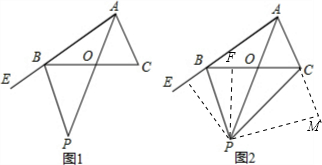 解:(1)如图1,设∠BA=2α,∠ACB=2β;
解:(1)如图1,设∠BA=2α,∠ACB=2β;
∵AP,BP分别平分∠BAC和∠CBE,
∴∠EBP=∠BPA+α,∠EBP=
(2α+2β),
∴∠BPA+α=α+β,故β=∠BPA=40°,
∴∠ACB=2β=80°.
(2)如图2,过点P作PE⊥AB、PF⊥BC、PM⊥AC
垂足分别为E、F、M;
∵AP,BP分别平分∠BAC和∠CBE,
∴PE=PM,PE=PF,
∴PM=PF,
∴PC平分∠BCM,
∴∠BCP=
=50°,
即∠BCP的度数为50°.
 解:(1)如图1,设∠BA=2α,∠ACB=2β;
解:(1)如图1,设∠BA=2α,∠ACB=2β;∵AP,BP分别平分∠BAC和∠CBE,
∴∠EBP=∠BPA+α,∠EBP=
| 1 |
| 2 |
∴∠BPA+α=α+β,故β=∠BPA=40°,
∴∠ACB=2β=80°.
(2)如图2,过点P作PE⊥AB、PF⊥BC、PM⊥AC
垂足分别为E、F、M;
∵AP,BP分别平分∠BAC和∠CBE,
∴PE=PM,PE=PF,
∴PM=PF,
∴PC平分∠BCM,
∴∠BCP=
| 180°-80° |
| 2 |
即∠BCP的度数为50°.
点评:该题主要考查了三角形的内角和定理、外角的性质及其应用问题;解题的关键是作辅助线,灵活解题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
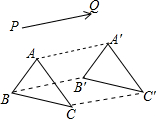 如图,△ABC沿PQ的方向平移到△A′B′C′的位置,AA′、BB′、CC′分别是对应点的连线,请问图中共有多少个平行四边形( )
如图,△ABC沿PQ的方向平移到△A′B′C′的位置,AA′、BB′、CC′分别是对应点的连线,请问图中共有多少个平行四边形( )| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,OP是∠AOB内任意一条射线,OM平分∠AOP,ON平分∠POB,∠MON=60°,求∠AOB的度数.
如图,OP是∠AOB内任意一条射线,OM平分∠AOP,ON平分∠POB,∠MON=60°,求∠AOB的度数. 如图,MN是⊙O的直径,MN=6,点B是ON上一动点,四边形ABCD和AEFG都是正方形,其中G、A在MN上,C、F在圆上,则正方形ABCD与正方形AEFG的面积和为( )
如图,MN是⊙O的直径,MN=6,点B是ON上一动点,四边形ABCD和AEFG都是正方形,其中G、A在MN上,C、F在圆上,则正方形ABCD与正方形AEFG的面积和为( )
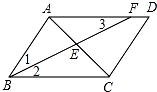 如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.
如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.