题目内容
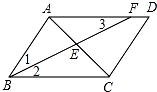 如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.
如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.(1)求证:AB=AF;
(2)当AB=3,BC=4时,求
| AE |
| AC |
考点:平行四边形的性质
专题:
分析:(1)由在平行四边形ABCD中,∠ABC的平分线BF,易证得∠1=∠3,即可证得:AB=AF;
(2)易证得△AEF∽△CEB,然后由相似三角形的对应边成比例,即可求得
的值.
(2)易证得△AEF∽△CEB,然后由相似三角形的对应边成比例,即可求得
| AE |
| AC |
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠3,
∵BF平分∠ABC,
∴∠1=∠2,
∴∠1=∠3,
∴AB=AF;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△AEF∽△CEB,
∴AE:CE=AF:BC,
∵AF=AB=3,BC=4,
∴AE:EC=3:4,
∴
=
.
∴AD∥BC,
∴∠2=∠3,
∵BF平分∠ABC,
∴∠1=∠2,
∴∠1=∠3,
∴AB=AF;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△AEF∽△CEB,
∴AE:CE=AF:BC,
∵AF=AB=3,BC=4,
∴AE:EC=3:4,
∴
| AE |
| AC |
| 3 |
| 7 |
点评:此题考查了平行四边形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
已知等腰三角形的一个外角等于100°,则它的顶角等于( )
| A、80° |
| B、50° |
| C、20°或50° |
| D、20°或80° |
已知y=1是方程2-
(m-y)=2y的解,则关于x的方程m(x+4)=m(2x+4)的解是( )
| 1 |
| 3 |
| A、x=1 | B、x=-1 |
| C、x=0 | D、方程无解 |

 如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,交AC于点G.
如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,交AC于点G.