题目内容
 如图,OP是∠AOB内任意一条射线,OM平分∠AOP,ON平分∠POB,∠MON=60°,求∠AOB的度数.
如图,OP是∠AOB内任意一条射线,OM平分∠AOP,ON平分∠POB,∠MON=60°,求∠AOB的度数.考点:角平分线的定义
专题:
分析:由角平分线的性质可得:∠AOP=2∠MOP,∠BOP=2∠PON,又因为∠AOB=∠AOP+∠BOP=2(∠MOP+∠PON)=2∠MON,然后将∠MON代入即可.
解答:解:∵OM平分∠AOP,ON平分∠POB,
∴∠AOP=2∠MOP,∠POB=2∠NOP,
∵∠AOB=∠AOP+∠BOP=2(∠MOP+∠PON)=2∠MON,∠MON=60°,
∴∠AOB=2×60°=120°.
∴∠AOP=2∠MOP,∠POB=2∠NOP,
∵∠AOB=∠AOP+∠BOP=2(∠MOP+∠PON)=2∠MON,∠MON=60°,
∴∠AOB=2×60°=120°.
点评:此题考查了角平分线的定义,解题的关键是:熟记角平分线的性质.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 数a,b,c在数轴上的对应点如图所示,且表示数a的点与表示数b的点到原点的距离相等.
数a,b,c在数轴上的对应点如图所示,且表示数a的点与表示数b的点到原点的距离相等.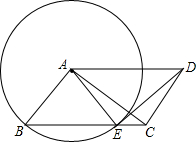 如图,在?ABCD中,AB⊥AC,以点A为圆心,AB为半径的圆交BC于点E.
如图,在?ABCD中,AB⊥AC,以点A为圆心,AB为半径的圆交BC于点E. 如图是由6个大小相同的小正方块搭成的一个几何体,则从左面所看到的形状图是( )
如图是由6个大小相同的小正方块搭成的一个几何体,则从左面所看到的形状图是( )




 如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,交AC于点G.
如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,交AC于点G.