题目内容
13.已知y1=x2-2x+3,y2=3x-k.(1)当x=1时,求出使等式y1=y2成立的实数k;
(2)若关于x的方程y1+k=y2有实数根,求k的取值范围.
分析 (1)把x=1代入y1=y2即x2-2x+3=3x-k,得关于k的方程,解方程可得k的值;
(2)由方程y1+k=y2即x2-2x+3+k=3x-k有实数根,可得△≥0,解不等式可得k的范围.
解答 解:(1)当x=1时,y1=2,y2=3-k,
根据题意,得:2=3-k,
解得:k=1;
(2)由题意,x2-2x+3+k=3x-k,即x2-5x+3+2k=0有实数根,
∴△=(-5)2-4(3+2k)≥0,
解得:k≤$\frac{13}{8}$.
点评 本题主要考查方程的解和一元二次方程根的判别式,根据方程的根的情况得出关于k的不等式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题: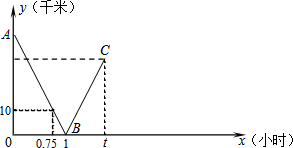 小明、小王二人骑车在平直的公路上分别从甲、乙两地相向而行,两人同时出发,匀速行驶.设行驶的时间为x(时),两人之间的距离为y(千米),小明到达乙地后立刻返回甲地,小王到达甲地后停止行驶,图中的折线表示从两人出发至小明到达乙地过程中y与x之间的函数关系.
小明、小王二人骑车在平直的公路上分别从甲、乙两地相向而行,两人同时出发,匀速行驶.设行驶的时间为x(时),两人之间的距离为y(千米),小明到达乙地后立刻返回甲地,小王到达甲地后停止行驶,图中的折线表示从两人出发至小明到达乙地过程中y与x之间的函数关系. 已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180°,得到△DEC.
已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180°,得到△DEC.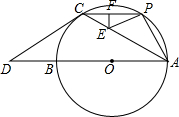 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA.
如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA. 如图,台阶阶梯每一层高20cm,宽40cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是多少?
如图,台阶阶梯每一层高20cm,宽40cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是多少?