题目内容
18.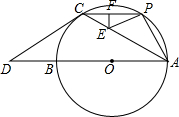 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA.
如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA.(1)求∠CAD的大小;
(2)已知P是$\widehat{AC}$的中点,E是线段AC上一点(不含端点,且AE>EC),作EF⊥PC,垂足为F,连接EP,当EF+EP的最小值为6时,求⊙O的半径.
分析 (1)连接OC,如图,由切线的性质得∠OCD=90°,再根据等腰三角形的性质得∠D=∠CAD,∠CAD=∠OCA,然后利用三角形内角和定理计算∠CAD的度数;
(2)连接OP,如图,利用圆周角定理得∠COD=2∠CAD=60°,则∠AOC=120°,再根据圆心角与弧的关系得到∠POC=∠AOP=60°,利用垂径定理得到OP⊥AC,则可判定△POC和△POA都是等边三角形,则AC垂直平分OP,OF交AC于E,如图,则EP=EO,利用两点之间线段最短得到OF=6,然后在Rt△POF中利用三角函数求OP的长即可.
解答 解:(1)连接OC,如图,
∵CD为切线,
∴OC⊥CD,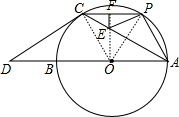
∴∠OCD=90°,
∵CD=CA,OC=OA,
∴∠D=∠CAD,∠CAD=∠OCA,
∵∠D+∠OCD+∠OCA+∠CAD=180°,
即∠CAD+90°+∠CAD+∠CAD=180°,
∴∠CAD=30°;
(2)连接OP,如图,
∵∠COD=2∠CAD=60°
∴∠AOC=120°,
∵P是$\widehat{AC}$的中点,
∴∠POC=∠AOP=60°,OP⊥AC,
∴△POC和△POA都是等边三角形,
∴AC垂直平分OP,
OF交AC于E,如图,则EP=EO,
∵EF+EP=EF+EO=OF,
∴此时EP+EF最小,即OF=6,
∵OF⊥PC,
∴∠PFO=90°,∠POF=$\frac{1}{2}∠$POC=30°
在Rt△POF中,∵cos∠POF=$\frac{OF}{OP}$,
∴OP=$\frac{6}{sin30°}$=4$\sqrt{3}$,
即⊙O的半径为4$\sqrt{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.解决本题的关键是证明△POC和△POA都是等边三角形.

| A. | mt2>nt2 | B. | mt2≥nt2 | C. | mt>nt | D. | mt<nt |

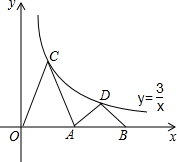 如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4.
如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4.