题目内容
1．计算：（1）6xy2•（-2x2y）÷（-3y3）
（2）[x（x2-2x+3）-3x]÷$\frac{1}{2}$x2．
分析 根据整式除法的运算方法，求出每个算式的值各是多少即可．
解答 解：（1）6xy2•（-2x2y）÷（-3y3）
=-12x3y3÷（-3y3）
=4x3
（2）[x（x2-2x+3）-3x]÷$\frac{1}{2}$x2
=[x3-2x2+3x-3x]÷$\frac{1}{2}$x2
=[x3-2x2]÷$\frac{1}{2}$x2
=2x-4
点评 此题主要考查了整式的除法，解答此题的关键是熟练掌握整式的除法法则：（1）单项式除以单项式，把系数，同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式．（2）多项式除以单项式，先把这个多项式的每一项分别除以单项式，再把所得的商相加．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
11．
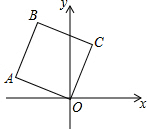如图，在正方形OABC中，点A的坐标是（-3，1），点B的纵坐标是4，则B，C两点的坐标分别是（ ）
如图，在正方形OABC中，点A的坐标是（-3，1），点B的纵坐标是4，则B，C两点的坐标分别是（ ）| A． | （-2，4），（1，3） | B． | （-2，4），（2，3） | C． | （-3，4），（1，4） | D． | （-3，4），（1，3） |
【材料阅读】阅读下列一段文字，然后回答下列问题．
9．
已知函数y=-x+4，回答下列问题：
（1）请在右图的直角坐标系中画出函数y=-x+4图象；
（2）y的值随x值的增大而减小；
（3）当y=2时，x的值为x=2；
（4）当y＜0时，x的取值范围是x＞4．
已知函数y=-x+4，回答下列问题：（1）请在右图的直角坐标系中画出函数y=-x+4图象；
（2）y的值随x值的增大而减小；
（3）当y=2时，x的值为x=2；
（4）当y＜0时，x的取值范围是x＞4．
6．
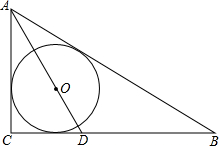如图，在Rt△ABC中，∠ACB=90°，周长为20，⊙O为△ABC内切圆，连接AO交BC于点D，且CD：BD=2：3，则△ABC内切圆的半径为（ ）
如图，在Rt△ABC中，∠ACB=90°，周长为20，⊙O为△ABC内切圆，连接AO交BC于点D，且CD：BD=2：3，则△ABC内切圆的半径为（ ）| A． | $\sqrt{5}$-1 | B． | $\sqrt{5}$+1 | C． | 3$\sqrt{5}$-5 | D． | 6$\sqrt{5}$-10 |
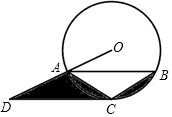如图，△ABC内接于⊙O，CA=CB，CD∥AB且与OA的延长线交于点D．
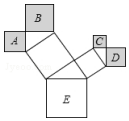如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、E的面积分别为2，5，1，10．则正方形D的面积是2．