题目内容
10．
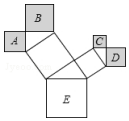如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、E的面积分别为2，5，1，10．则正方形D的面积是2．
分析 分别设中间两个正方形和正方形D的面积为x，y，z，由勾股定理即可得到结论．
解答 解：设中间两个正方形的面积分别为x、y，正方形D的面积为z，则由勾股定理得：
x=2+5=7；
y=1+z；
7+y=7+1+z=10；
即正方形D的面积为：z=2．
故答案为：2．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
5．下列四个关系式中，y是x的反比例函数的是（ ）
| A． | y=4x | B． | y=$\frac{1}{3x}$ | C． | y=$\frac{1}{{x}^{2}}$ | D． | y=$\frac{1}{x+1}$ |
15．
实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）
实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）| A． | b＜a | B． | ab＞0 | C． | |b|＜|a| | D． | a+b=0 |
