Question

6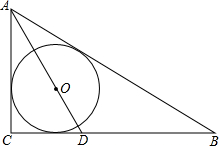．如图，在Rt△ABC中，∠ACB=90°，周长为20，⊙O为△ABC内切圆，连接AO交BC于点D，且CD：BD=2：3，则△ABC内切圆的半径为（　　）

• A． $\sqrt{5}$-1
• B． $\sqrt{5}$+1
• C． 3$\sqrt{5}$-5
• D． 6$\sqrt{5}$-10

Answer 1

分析 根据内心的性质、角平分线的性质得到CA：BA=2：3，根据三角形的周长公式列出方程求出x，根据内切圆的半径公式计算即可．

解答 解：∵⊙O为△ABC内切圆，
∴AD平分∠CAB，
∵CD：BD=2：3，
∴CA：BA=2：3，
设CA、BA分别为2x、3x，
由勾股定理得，BC=$\sqrt{5}$x，
则2x+3x+$\sqrt{5}$x=20，
解得，x=5-$\sqrt{5}$，
∴AC=10-2$\sqrt{5}$，AB=15-3$\sqrt{5}$，BC=5$\sqrt{5}$-5，
∴△ABC内切圆的半径为$\frac{10-2\sqrt{5}+5\sqrt{5}-5-15+3\sqrt{5}}{2}$=3$\sqrt{5}$-5，
故选：C．

点评 本题考查的是三角形的内切圆和内心，掌握角平分线的性质、内心的性质、三角形的内切圆的半径的求法是解题的关键．