题目内容
12. 【材料阅读】阅读下列一段文字,然后回答下列问题.
【材料阅读】阅读下列一段文字,然后回答下列问题.已知平面内两点M(x1,y1),N(x2,y2),则这两点间的距离可用下列公式计算:
MN=$\sqrt{{(x}_{1}{-x}_{2})^{2}+{(y}_{1}{-y}_{2})^{2}}$.
例如:已知P(3,1)、Q(1,-2),则这两点间的距离PQ=$\sqrt{(3-1)^{2}+(1+2)^{2}}$=$\sqrt{13}$
【直接应用】
(1)已知A(2,-3)、B(-4,5),试求A、B两点间的距离;
(2)已知△ABC的顶点坐标分别为A(0,4)、B(-1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
【深度应用】
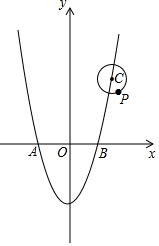
(3)如图,在平面直角坐标系xOy中,二次函数y=x2-4的图象与x轴相交于两点A、B,(点A在点B的左边)
①求点A、B的坐标;
②设点P(m,n)是以点C(3,4)为圆心,1为半径的圆上一动点,求PA2+PB2的最大值.
分析 (1)依据两点间的距离公式可求得AB的长;
(2)依据两点间的距离公式可求得AB、AC、BC的长,然后依据勾股定理的逆定理可对△ABC的形状作出判断;
(3)①令y=0得:x2-4=0,解得x=2或x=-2,故此可得到A,B的坐标;②首先依据两点间的距离公式表示出PA2+PB2的长,通过化简可得到PA2+PB2=2PO2+8,然后求得OP的最大值,从而可得到问题的答案.
解答 解:(1)AB=$\sqrt{[2-(-4)]^{2}+(-3-5)^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
(2)AB2=(-1-0)2+(2-4)2=1+4=5;
AC2=(0-4)2+(4-2)2=16+4=20;BC2=(-1-4)2+(2-2)2=25,
∴BC2=AB2+AC2.
∴△ABC为直角三角形.
(3)①令y=0得:x2-4=0,解得x=2或x=-2,
∴A(-2,0),B(2,0).
②PA2+PB2=(m+2)2+n2+(m-2)2+n2=2(m2+n2)+8=2PO2+8.
当OP过圆心C时,PO最大,最大值=OC+PC=5+1=6.
因此PA2+PB2最大值为2×62+8=80.
点评 本题主要考查的是二次函数的综合、两点间的距离公式,依据两点间的距离公式得到PA2+PB2=2PO2+8是解题的关键.

练习册系列答案
相关题目
3.若函数y=2x2-8x+m的图象上有两点A(x1,y1),B(x2,y2),若x1<x2<-2,则( )
| A. | y1<y2 | B. | y1>y2 | ||
| C. | y1=y2 | D. | y1、y2、的大小不确定 |
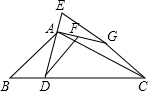 如图,在△ABC中,∠B=45°,∠ACB=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,点F在线段AG上,延长DA至点E,使AE=AF,连接EG,CG,DF,若EG=DF,点G在AC的垂直平分线上,则$\frac{AB}{CG}$的值为$\frac{\sqrt{3}+1}{2}$.
如图,在△ABC中,∠B=45°,∠ACB=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,点F在线段AG上,延长DA至点E,使AE=AF,连接EG,CG,DF,若EG=DF,点G在AC的垂直平分线上,则$\frac{AB}{CG}$的值为$\frac{\sqrt{3}+1}{2}$.