题目内容
11.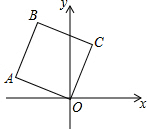 如图,在正方形OABC中,点A的坐标是(-3,1),点B的纵坐标是4,则B,C两点的坐标分别是( )
如图,在正方形OABC中,点A的坐标是(-3,1),点B的纵坐标是4,则B,C两点的坐标分别是( )| A. | (-2,4),(1,3) | B. | (-2,4),(2,3) | C. | (-3,4),(1,4) | D. | (-3,4),(1,3) |
分析 作CD⊥x轴于D,作AE⊥x轴于E,作BF⊥AE于F,由AAS证明△AOE≌△OCD,得出AE=OD,OE=CD,由点A的坐标是(-3,1),得出OE=3,AE=1,∴OD=1,CD=3,得出C(1,3),同理:△AOE≌△BAF,得出AE=BF=1,OE-BF=3-1=2,得出B(-2,4)即可.
解答  解:如图所示:作CD⊥x轴于D,作AE⊥x轴于E,作BF⊥AE于F,
解:如图所示:作CD⊥x轴于D,作AE⊥x轴于E,作BF⊥AE于F,
则∠AEO=∠ODC=∠BFA=90°,
∴∠OAE+∠AOE=90°,
∵四边形OABC是正方形,
∴OA=CO=BA,∠AOC=90°,
∴∠AOE+∠COD=90°,
∴∠OAE=∠COD,
在△AOE和△OCD中,$\left\{\begin{array}{l}{∠AEO=∠ODC}&{\;}\\{∠OAE=∠COD}&{\;}\\{OA=CO}&{\;}\end{array}\right.$,
∴△AOE≌△OCD(AAS),
∴AE=OD,OE=CD,
∵点A的坐标是(-3,1),
∴OE=3,AE=1,
∴OD=1,CD=3,
∴C(1,3),
同理:△AOE≌△BAF,
∴AE=BF=1,OE-BF=3-1=2,
∴B(-2,4);
故选:A.
点评 本题考查了正方形的性质、全等三角形的判定与性质、坐标与图形性质;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | D. | $\sqrt{3}$÷$\sqrt{12}$=$\frac{1}{2}$ |
3.若函数y=2x2-8x+m的图象上有两点A(x1,y1),B(x2,y2),若x1<x2<-2,则( )
| A. | y1<y2 | B. | y1>y2 | ||
| C. | y1=y2 | D. | y1、y2、的大小不确定 |