题目内容
11.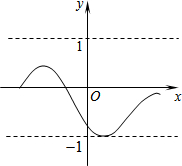 对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界值1.若函数y=-x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,则b的取值范围是-1<b≤3.
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界值1.若函数y=-x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,则b的取值范围是-1<b≤3.
分析 根据函数的增减性、边界值确定a=-1;然后由“函数的最大值也是2”来求b的取值范围.
解答 解:∵k=-1,y随x的增大而减小,
∴当x=a时,-a+1=2,解得a=-1,
而x=b时,y=-b+1,
∴-2≤-b+1≤2,
且b>a,
∴-1<b≤3.
故答案为-1<b≤3.
点评 本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.

练习册系列答案
相关题目
1.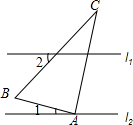 如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
 如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
1.已知点A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(4、2)中有三个点在关于x的二次函数y=a(x-1)2+k(a>0)的图象上,请结合你学过的抛物线的知识挑选你认为正确的三个点( )
| A. | A、C、E | B. | B、C、D | C. | B、C、E | D. | A、B、D |
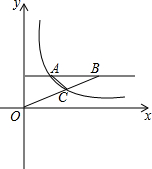 如图,反比例函数y=$\frac{6}{x}$(x>0)上任取一点A,过A作AB∥x轴,OB交图象于C,OC:BC=2:3,求△ABC面积.
如图,反比例函数y=$\frac{6}{x}$(x>0)上任取一点A,过A作AB∥x轴,OB交图象于C,OC:BC=2:3,求△ABC面积.