题目内容
20.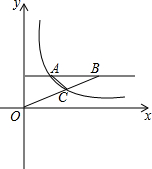 如图,反比例函数y=$\frac{6}{x}$(x>0)上任取一点A,过A作AB∥x轴,OB交图象于C,OC:BC=2:3,求△ABC面积.
如图,反比例函数y=$\frac{6}{x}$(x>0)上任取一点A,过A作AB∥x轴,OB交图象于C,OC:BC=2:3,求△ABC面积.
分析 设C(a,$\frac{6}{a}$).易求B($\frac{5}{2}$a,$\frac{15}{a}$)、点A的纵坐标是$\frac{15}{a}$.把点A的纵坐标代入y=$\frac{6}{x}$可以求得点A的横坐标;由点A、B的坐标可以求得线段AB的长度,由点B、C的纵坐标可以求得AB边上高的长度,所以根据三角形的面积公式进行解答即可.
解答 解:设C(a,$\frac{6}{a}$).
∵OC:BC=2:3,
∴OB=$\frac{5}{2}$OC,
∴B($\frac{5}{2}$a,$\frac{15}{a}$).
∵AB∥x轴,点A在反比例函数y=$\frac{6}{x}$(x>0)上,
∴点A的纵坐标是$\frac{15}{a}$.
把y=$\frac{15}{a}$代入y=$\frac{6}{x}$,得
x=$\frac{2}{5}$a.
∴△ABC面积是:$\frac{1}{2}$($\frac{5}{2}$a-$\frac{2}{5}$a)•($\frac{15}{a}$-$\frac{6}{a}$)=$\frac{189}{20}$.
点评 本题考查了反比例函数图象上点的坐标特征.此题实际上是反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.

练习册系列答案
相关题目
5.下列计算中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | (-$\frac{1}{3}$)-1=-3 | C. | 2a+3b=5ab | D. | a6÷a2=a3 |
9.下列各运算中,计算正确的是( )
| A. | 3x2+5x2=8x4 | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | ||
| C. | $\frac{1}{x+1}$-$\frac{1}{x-1}$=$\frac{2}{{{x^2}-1}}$ | D. | (-$\frac{1}{2}$m2n)2=$\frac{1}{4}$m4n2 |
10. 若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )
若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )
 若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )
若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )| A. | 78π | B. | 51π | C. | 36π | D. | 24π |
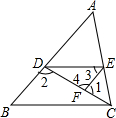 如图,已知∠1+∠2=180°,∠3=∠B,
如图,已知∠1+∠2=180°,∠3=∠B,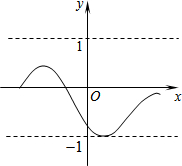 对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界值1.若函数y=-x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,则b的取值范围是-1<b≤3.
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界值1.若函数y=-x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,则b的取值范围是-1<b≤3.
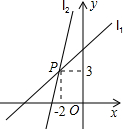 如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集是x<-2.
如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集是x<-2.