题目内容
6.如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的长度是12.5 米,MN是二楼楼顶,MN∥PQ,C是MN 上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角∠CAQ为45°,坡角∠BAQ为37°,求二楼的层高BC(精确到0.1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 )
分析 延长CB交PQ于点D,根据坡度角的度数求得BD的长,然后在直角△CDA中利用三角函数即可求得CD的长,则BC即可得到.
解答 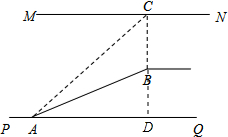 解:延长CB交PQ于点D,
解:延长CB交PQ于点D,
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵坡角∠BAQ为37°,
∴$\frac{BD}{AD}$=tan37°≈0.75=$\frac{3}{4}$,
设BD=3x米,AD=4x米,则AB=5x米.
∵AB=12.5米,
∴x=2.5,
∴BD=7.5米,AD=10米.
在Rt△CDA中,∠CDA=90゜,∠CAQ=45°,
∴CD=AD=10米,
∴BC=CD-BD=10-7.5=2.5(米).
答:二楼的层高BC约为2.5米.
点评 本题考查了解直角三角形的应用,用到的知识点是特殊角的三角函数值、仰角和坡度的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
18.观察下表
请你结合该表格及相关知识,求出b,c的值,并验证13,b,c是否是勾股数?
| 列 举 | 猜 想 |
| 3、4、5 | 32=4+5 |
| 5、12、13 | 52=12+13 |
| 7、24、25 | 72=24+25 |
| … | … |
| 13、b、c | 132=b+c |
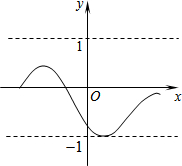 对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界值1.若函数y=-x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,则b的取值范围是-1<b≤3.
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界值1.若函数y=-x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,则b的取值范围是-1<b≤3.
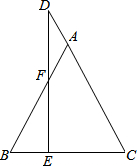 已知:如图,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交线段AB于点F.请找出一组相等的线段(AB=AC除外)并加以证明.
已知:如图,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交线段AB于点F.请找出一组相等的线段(AB=AC除外)并加以证明.