如图.在?ABCD中.CE⊥AB.E为垂足.如果∠BCE=35°.则∠D的度数为( )A．55°B．35°C．25°D．30° 题目和参考答案——青夏教育精英家教网—

题目内容

4．

如图，在?ABCD中，CE⊥AB，E为垂足，如果∠BCE=35°，则∠D的度数为（　　）

A．

55°

B．

35°

C．

25°

D．

30°

分析首先利用直角三角形的性质得出∠B的度数，再利用平行四边形的对角相等，进而得出答案．

解答解：∵CE⊥AB，∠BCE=35°，
∴∠B=90°-35°=55°，
∵四边形ABCD是平行四边形，
∴∠D=∠B=55°．
故选：A．

点评此题主要考查了平行四边形的性质、直角三角形的性质，正确掌握平行四边形的性质是解题关键．

练习册系列答案

15．如图1，在平面直角坐标系中，A（a，0）是x轴正半轴上一点，C是第四象限一点，CB⊥y轴，交y轴负半轴于B（0，b），且（a-3）²+|b+4|=0，S_{四边形AOBC}=16．
（1）求C点坐标；
（2）如图2，设D为线段OB上一动点，当AD⊥AC时，∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P，求∠APD的度数．
（3）如图3，当D点在线段OB上运动时，作DM⊥AD交BC于M点，∠BMD、∠DAO的平分线交于N点，则D点在运动过程中，∠N的大小是否变化？若不变，求出其值，若变化，说明理由．

12．已知一元二次方程（a-1）x²+7ax+a²+3a-4=0有一个根为零，则a=-4．

19．已知如图，四边形ABCD，BE、DF分别平分四边形的外角∠MBC和∠NDC，若∠BAD=α，∠BCD=β
（1）如图1，若α+β=150°，求∠MBC+∠NDC的度数；
（2）如图1，若BE与DF相交于点G，∠BGD=45°，请写出α、β所满足的等量关系式；
（3）如图2，若α=β，判断BE、DF的位置关系，并说明理由．

9．如图1，已知射线CB∥OA，∠C=∠OAB=120°，E₁，F在CB上，且满足∠FOB=∠FBO，OE₁平分∠COF．
（1）求∠E₁OB的度数；
（2）若向右平行移动AB，其它条件不变，那么∠OBC：∠OFC的值是否发生变化？若变化，找出其中规律，若不变，求出这个比值；
（3）如图2，若OE₂平分∠COE₁交CB于E₂，OE₃平分∠COE₂交CB于E₃，…，以此类推直到OE_n平分∠COE_n-1．若∠BOA=x，当n=4时，求∠OE₄C．

16．用反证法证明“同一平面内，若a⊥c，b⊥c，则a∥b”时应假设（　　）

13．

如图，△ABD≌△CDB，下面四个结论中不正确的是（　　）

	A．	△ABD和△CDB的面积相等		B．	△ABD和△CDB的周长相等
	C．	∠A+∠ABD=∠C+∠CBD		D．	AD∥BC，且AD=BC

14．

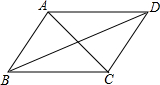如图，下列条件不能够判定AB∥DC的是（　　）

试题分类