题目内容
19.已知如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β(1)如图1,若α+β=150°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请写出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
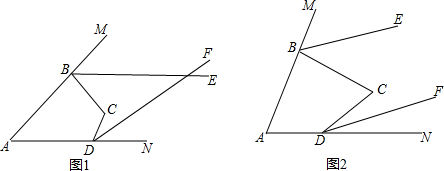
分析 (1)利用角平分线的定义和四边形的内角和以及α+β=150°推导即可;
(2)利用角平分线的定义和四边形的内角和以及三角形的内角和转化即可;
(3)利用角平分线的定义和四边形的内角和以及三角形的外角的性质计算即可.
解答 解:(1)在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠ABC+∠ADC=360°-(α+β),
∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)=360°-[360°-(α+β)]=α+β,
∵α+β=150°,
∴∠MBC+∠NDC=150°,
(2)β-α=90°
理由:如图1,连接BD,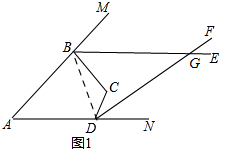
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=$\frac{1}{2}$∠MBC,∠CDG=$\frac{1}{2}$∠NDC,
∴∠CBG+∠CDG=$\frac{1}{2}$∠MBC+$\frac{1}{2}$∠NDC=$\frac{1}{2}$(∠MBC+∠NDC)=$\frac{1}{2}$(α+β),
在△BCD中,∠BDC+∠CDB=180°-∠BCD=180°-β,
在△BDG中,∠BGD=45°,
∴∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,
∴$\frac{1}{2}$(α+β)+180°-β+45°=180°,
∴β-α=90°,
(3)平行,
理由:如图2,延长BC交DF于H,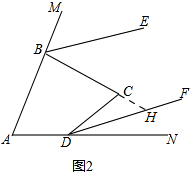
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=$\frac{1}{2}$∠MBC,∠CDH=$\frac{1}{2}$∠NDC,
∴∠CBE+∠CDH=$\frac{1}{2}$∠MBC+$\frac{1}{2}$∠NDC=$\frac{1}{2}$(∠MBC+∠NDC)=$\frac{1}{2}$(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD-∠DHB=β-∠DHB,
∴∠CBE+β-∠DHB=$\frac{1}{2}$(α+β),
∵α=β,
∴∠CBE+β-∠DHB=$\frac{1}{2}$(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
点评 此题是三角形综合题,主要考查了平角的意义,四边形的内角和,三角形内角和,三角形的外角的性质,角平分线的意义,用整体代换的思想是解本题的关键,整体思想是初中阶段的一种重要思想,要多加强训练.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案①内错角相等;
②对顶角相等;
③对于任意实数x,代数式x2-6x+10总是正数;
④若三条线段a、b、c满足a+b>c,则三条线段a、b、c一定能组成三角形.
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 1 |
 如图,在?ABCD中,CE⊥AB,E为垂足,如果∠BCE=35°,则∠D的度数为( )
如图,在?ABCD中,CE⊥AB,E为垂足,如果∠BCE=35°,则∠D的度数为( )| A. | 55° | B. | 35° | C. | 25° | D. | 30° |
 如图OA⊥OB,若∠BOC=40°,则∠AOC的度数是( )
如图OA⊥OB,若∠BOC=40°,则∠AOC的度数是( )| A. | 20° | B. | 40° | C. | 50° | D. | 60° |
| A. | 若 a、b、c是△ABC的三边,则a2+b2=c2 | |
| B. | 若 a、b、c是Rt△ABC的三边,则a2+b2=c2 | |
| C. | 若 a、b、c是Rt△ABC的三边,∠A=90°,则a2+b2=c2 | |
| D. | 若 a、b、c是Rt△ABC的三边,∠C=90°,则a2+b2=c2 |