题目内容
15.如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.(1)求C点坐标;
(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.
(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.

分析 (1)利用非负数的和为零,各项分别为零,求出a,b即可;
(2)用同角的余角相等和角平分线的意义即可;
(3)利用角平分线的意义和互余两角的关系简单计算证明即可.
解答 解:(1)∵(a-3)2+|b+4|=0,
∴a-3=0,b+4=0,
∴a=3,b=-4,
∴A(3,0),B(0,-4),
∴OA=3,OB=4,
∵S四边形AOBC=16.
∴$\frac{1}{2}$(OA+BC)×OB=16,
∴$\frac{1}{2}$(3+BC)×4=16,
∴BC=5,
∵C是第四象限一点,CB⊥y轴,
∴C(5,-4)
(2)如图,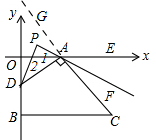
延长CA,
∵AF是∠CAE的角平分线,
∴∠CAF=$\frac{1}{2}$∠CAE,
∵∠CAE=∠OAG,
∴∠CAF=$\frac{1}{2}$∠OAG,
∵AD⊥AC,
∴∠DAO+∠OAG=∠PAD+∠PAG=90°,
∵∠AOD=90°,
∴∠DAO+∠ADO=90°,
∴∠ADO=∠OAG,
∴∠CAF=$\frac{1}{2}$∠ADO,
∵DP是∠ODA的角平分线
∴∠ADO=2∠ADP,
∴∠CAF=∠ADP,
∵∠CAF=∠PAG,
∴∠PAG=∠ADP,
∴∠APD=180°-(∠ADP+∠PAD)=180°-(∠PAG+∠PAD)=180°-90°=90°
即:∠APD=90°
(3)不变,∠ANM=45°
理由:如图,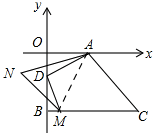
∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∵DM⊥AD,
∴∠ADO+∠BDM=90°,
∴∠DAO=∠BDM,
∵NA是∠OAD的平分线,
∴∠DAN=$\frac{1}{2}$∠DAO=$\frac{1}{2}$∠BDM,
∵CB⊥y轴,
∴∠BDM+∠BMD=90°,
∴∠DAN=$\frac{1}{2}$(90°-∠BMD),
∵MN是∠BMD的角平分线,
∴∠DMN=$\frac{1}{2}$∠BMD,
∴∠DAN+∠DMN=$\frac{1}{2}$(90°-∠BMD)+$\frac{1}{2}$∠BMD=45°
在△DAM中,∠ADM=90°,
∴∠DAM+∠DMA=90°,
在△AMN中,
∠ANM=180°-(∠NAM+∠NMA)
=180°-(∠DAN+∠DAM+∠DMN+∠DMA)
=180°-[(∠DAN+DMN)+(∠DAM+∠DMA)]
=180°-(45°+90°)
=45°,
∴D点在运动过程中,∠N的大小不变,求出其值为45°
点评 此题是四边形综合题,主要考查了非负数的性质,四边形的面积的计算方法,角平分线的意义,解本题的关键是用整体思想解决问题,也是本题的难点.

| A. | y=(x+2)2+1 | B. | y=(x+2)2-1 | C. | y=(x-2)2-1 | D. | y=(x-2)2+1 |
①内错角相等;
②对顶角相等;
③对于任意实数x,代数式x2-6x+10总是正数;
④若三条线段a、b、c满足a+b>c,则三条线段a、b、c一定能组成三角形.
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 3.5×104米 | B. | 3.5×10-4米 | C. | 3.5×10-5米 | D. | 3.5×10-9米 |
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 1 |
 如图,在?ABCD中,CE⊥AB,E为垂足,如果∠BCE=35°,则∠D的度数为( )
如图,在?ABCD中,CE⊥AB,E为垂足,如果∠BCE=35°,则∠D的度数为( )| A. | 55° | B. | 35° | C. | 25° | D. | 30° |
 如图,已知直线a∥b,∠1=55°,则∠2的度数是( )
如图,已知直线a∥b,∠1=55°,则∠2的度数是( )| A. | 35° | B. | 55° | C. | 125° | D. | 145° |