题目内容

13．如图，△ABD≌△CDB，下面四个结论中不正确的是（　　）
A．△ABD和△CDB的面积相等B．△ABD和△CDB的周长相等
C．∠A+∠ABD=∠C+∠CBDD．AD∥BC，且AD=BC

分析 根据全等三角形的面积相等，全等三角形的周长相等，全等三角形对应角相等，全等三角形对应边相等对各选项分析判断即可得解．

解答 解：∵△ABD≌△CDB，
∴∠ADB=∠CBD，AD=BC，△ABD和△CDB的面积相等，△ABD和△CDB的周长相等，
∴AD∥BC，
则选项A，B，D一定正确．
由△ABD≌△CDB不一定能得到∠ABD=∠CBD，因而∠A+∠ABD=∠C+∠CBD不一定成立．
故选C．

点评 本题考查了全等三角形的性质，熟记性质并准确识图确定出对应角和对应边是解题的关键．

练习册系列答案
相关题目
3．下列各式中是一元一次方程的有（　　）
①x2-4x       ②3x-1=$\frac{x}{2}$         ③x+2y        ④xy-3       ⑤5x-x=3．
A．2个B．3个C．4个D．5个
4．如图，在?ABCD中，CE⊥AB，E为垂足，如果∠BCE=35°，则∠D的度数为（　　）
A．55°B．35°C．25°D．30°
1．如图，平行四边形ABCD的对角线AC、BD相交于点O，若AC+BD=10，BC=4，则△BOC的周长为（　　）
A．8B．9C．10D．14
8．如图所示，将两个正方形ABCD和正方形CGEF如图所示放置，连接DE、BG．
（1）图中∠DCE+∠BCG=180°；
（2）设△DCE的面积为s1，△BCG的面积为s2，则s1与s2的数量关系为S1=S2；
猜想论证：
如图2所示，将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG，连接DE、BG，设△DCE的面积为s1，△BCG的面积为s2，猜想s1和s2的数量关系，并加以证明？
如图3所示，在△ABC中，AB=AC=10cm，∠B=30°，把△ABC沿AC翻折得到△AEC，过点A作AD平行CE交BC于点D，在线段CE上存在点△P，使△ABP的面积等于△ACD的面积，请写出CP的长？
18．如图，平行四边形ABCD中，EF∥BC，AE：EB=2：3，EF=4，则AD的长为（　　）
A．$\frac{16}{3}$B．8C．10D．16
5．如图，已知直线a∥b，∠1=55°，则∠2的度数是（　　）
A．35°B．55°C．125°D．145°
2．如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x＜ax+4的解集为（　　）
A．x＜3B．$x＞\frac{3}{2}$C．x＜$\frac{3}{2}$D．x＞3
3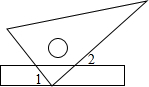．小红把一把直尺与一块三角板如图放置，测得∠1=48°，则∠2的度数为（　　）
A．38°B．42°C．48°D．52°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网