题目内容
14．
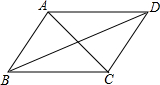如图，下列条件不能够判定AB∥DC的是（ ）| A． | ∠BAC=∠ACD | B． | ∠DCB+∠ABC=180° | C． | ∠ABD=∠BDC | D． | ∠DAC=∠BCA |
分析 根据平行线的判定定理对各选项进行逐一判断即可．
解答 解：A、∵∠BAC=∠ACD，∴AB∥CD，故本选项错误；
B、∵∠DCB+∠ABC=180°，∴AB∥CD，故本选项错误；
C、∵∠ABD=∠BDC，∴AB∥CD，故本选项错误；
D、∵∠DAC=∠BCA，∴AD∥BC，故本选项正确．
故选D．
点评 本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．
如图，在?ABCD中，CE⊥AB，E为垂足，如果∠BCE=35°，则∠D的度数为（ ）
如图，在?ABCD中，CE⊥AB，E为垂足，如果∠BCE=35°，则∠D的度数为（ ）| A． | 55° | B． | 35° | C． | 25° | D． | 30° |
5．
如图，已知直线a∥b，∠1=55°，则∠2的度数是（ ）
如图，已知直线a∥b，∠1=55°，则∠2的度数是（ ）| A． | 35° | B． | 55° | C． | 125° | D． | 145° |
2．
如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x＜ax+4的解集为（ ）
如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x＜ax+4的解集为（ ）| A． | x＜3 | B． | $x＞\frac{3}{2}$ | C． | x＜$\frac{3}{2}$ | D． | x＞3 |
9．下列说法正确的是（ ）
| A． | 若 a、b、c是△ABC的三边，则a2+b2=c2 | |
| B． | 若 a、b、c是Rt△ABC的三边，则a2+b2=c2 | |
| C． | 若 a、b、c是Rt△ABC的三边，∠A=90°，则a2+b2=c2 | |
| D． | 若 a、b、c是Rt△ABC的三边，∠C=90°，则a2+b2=c2 |
19．
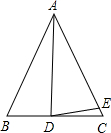如图，在△ABC中，AB=AC，AD=AE，∠BAD=30°，∠EDC的度数是（ ）
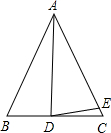如图，在△ABC中，AB=AC，AD=AE，∠BAD=30°，∠EDC的度数是（ ）| A． | 10° | B． | 15° | C． | 20° | D． | 25° |
6．下列方程没有实数根的是（ ）
| A． | x2+4x=10 | B． | 3x2+8x-3=0 | C． | x2-2x+3=0 | D． | （x-2）（x-3）=12 |
3．
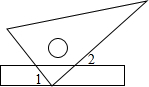小红把一把直尺与一块三角板如图放置，测得∠1=48°，则∠2的度数为（ ）
小红把一把直尺与一块三角板如图放置，测得∠1=48°，则∠2的度数为（ ）| A． | 38° | B． | 42° | C． | 48° | D． | 52° |
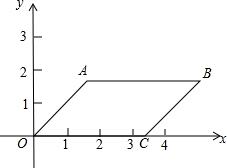如图，在平行四边形OABC中，已知AB=OC，AB∥OC．A、C两点的坐标分别为$A（\sqrt{3}，\sqrt{3}），C（2\sqrt{3}，0）$．