题目内容
嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD，并写出了如下不完整的已知和求证．
已知：如图1，在四边形ABCD中，BC=AD，AB=
求证：四边形ABCD是 四边形．
（1）在方框中填空，以补全已知和求证；
（2）按嘉淇同学的思路写出证明过程；
（3）用文字叙述所证命题的逆命题.
（1）见解析；（2）见解析
【解析】试题分析：（1）命题的题设为“两组对边分别相等的四边形”，结论是“是平行四边形”，即可得到结论；
（2）连接BD，利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC，∠ABD=∠CDB，进而可得AB∥CD，AD∥CB，根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形；
（3）把命题“两组对边分别相等的四边形是平行四...
金牌课堂练系列答案
三新快车金牌周周练系列答案有一个两位数，个位上的数字为a，十位上的数字为b，如果把这个两位数的个位与十位上的数字对调，得到的两位数大于原来的两位数，那么a与b哪个大？
a＞b
【解析】试题分析：根据题意得到不等式10b+a＜10a+b，通过解该不等式即可比较它们的大小．
试题解析：根据题意，得
10b+a＜10a+b，
所以，9b＜9a，
所以，b＜a，即a＞b． 如图，A与A′关于直线MN对称，P是BA′与MN的交点.若P1为直线MN上任意一点（不与P重合），连结AP1、BP1，试说明 AP1+BP1>AP+BP.
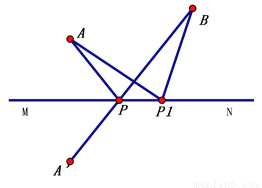
见解析
【解析】试题分析：由三角形三条边的关系可得A′P1+BP1>A′B，再由轴对称的性质可得AP1=A′P1，然后通过等量代换可证明结论.
【解析】
如图，连结AP1，则在△A′P1B中，有A′P1+BP1>A′B
∴A′P1+BP1>A′P+PB
∵A与A′关于直线MN对称，
∴AP1与A′P1关于直线MN对称
∴AP1=A′P1
同理可得：AP=... 两个图形关于某直线对称，对称点一定( )
A. 这直线的两旁 B. 这直线的同旁 C. 这直线上 D. 这直线两旁或这直线上
D
【解析】由成轴对称的定义知，成轴对称的两个图形的对称点，或者在对称轴上，或者在对称轴两旁.
故选D. 下列说法正确的是( )
A. 两个全等的三角形一定关于某条直线对称 B. 关于某条直线的对称的两个三角形一定全等
C. 直角三角形是轴对称图形 D. 锐角三角形都是轴对称图形
B
【解析】A.根据轴对称的定义，全等三角形不一定关于某直线对称，故错误；
B. 根据轴对称的性质,关于某条直线的对称的两个三角形一定全等,故正确;
C.直角三角形中，等腰直角三角形是轴对称图形，其它一般的直角三角形不是，故错误；
D.锐角三角形不一定是轴对称图形，如三个角分别是50°、60°、70°的三角形就不是轴对称图形，故错误.
故选B. 如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件_________
（只添一个即可），使四边形ABCD是平行四边形
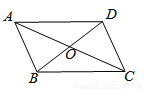
BO=DO
【解析】【解析】
∵AO=CO，BO=DO，∴四边形ABCD是平行四边形．故答案为：BO=DO． (吉安永新县期末)如图，在四边形ABCD中，AB∥DC，AD＝BC＝5，DC＝7，AB＝13，点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动．当四边形PQBC为平行四边形时，运动时间为( )
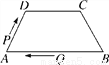
A. 4s B. 3s C. 2s D. 1s
B
【解析】试题解析：设运动时间为t秒，则CP=12-3t，BQ=t，
根据题意得到12-3t=t，
解得：t=3，
故选B． 袋中有红球4个,白球若干个,它们只有颜色上的区别,从袋中随机地取出一个球,如果取得白球的可能性较大,那么袋中白球可能有( )
A. 3个 B. 不足3个
C. 4个 D. 5个或5个以上
D
【解析】根据取到白球的可能性较大可以判断出白球的数量大于红球的数量，从而得解．
【解析】
∵袋中有红球4个，取到白球的可能性较大，
∴袋中的白球数量大于红球数量，
即袋中白球的个数可能是5个或5个以上．
故选D．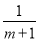 
与
的最简公分母是__________
【解析】试题分析：m2－1＝(m＋1)(m－1)，
所以最简公分母是m2－1．
故答案为：m2－1．