��Ŀ����
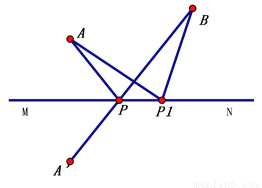
��ͼ��A��A�����ֱ��MN�Գƣ�P��BA����MN�Ľ���.��P1Ϊֱ��MN������һ�㣨����P�غϣ�������AP1��BP1����˵�� AP1+BP1>AP+BP.
 ������
������������������������������ߵĹ�ϵ�ɵ�A��P1+BP1>A��B��������ԳƵ����ʿɵ�AP1=A��P1��Ȼ��ͨ������������֤������.
��������
��ͼ������AP1�����ڡ�A��P1B�У���A��P1+BP1>A��B
��A��P1+BP1>A��P+PB
��A��A�����ֱ��MN�Գƣ�
��AP1��A��P1����ֱ��MN�Գ�
��AP1=A��P1
ͬ���ɵã�AP=...
������
������������������������������ߵĹ�ϵ�ɵ�A��P1+BP1>A��B��������ԳƵ����ʿɵ�AP1=A��P1��Ȼ��ͨ������������֤������.
��������
��ͼ������AP1�����ڡ�A��P1B�У���A��P1+BP1>A��B
��A��P1+BP1>A��P+PB
��A��A�����ֱ��MN�Գƣ�
��AP1��A��P1����ֱ��MN�Գ�
��AP1=A��P1
ͬ���ɵã�AP=...
 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д������ε��ڽǺ��ǣ� ��
A��540�� B��720�� C��900�� D��360��
 B��
��������
������������ݶ���ε��ڽǺ�ʽ�ɵ������ε��ڽǺ��ǣ�6��2����180��=720�㣬�ʴ�ѡB��
B��
��������
������������ݶ���ε��ڽǺ�ʽ�ɵ������ε��ڽǺ��ǣ�6��2����180��=720�㣬�ʴ�ѡB�� ���в��ȹ�ϵһ����ȷ���ǣ� ��
A.|a|��0 B.��x2��0 C.��x+1��2��0 D.a2��0
 C
��������
������������ݾ���ֵ����ȫƽ��ʽ��������⣮
��������
A��|a|��0������
B����x2��0������
C����x+1��2��0����ȷ��
D��a2��0������
��ѡC��
C
��������
������������ݾ���ֵ����ȫƽ��ʽ��������⣮
��������
A��|a|��0������
B����x2��0������
C����x+1��2��0����ȷ��
D��a2��0������
��ѡC�� ��ͼ����ABC�͡�A��B��C�����ֱ��l�Գƣ����н����У�
�١�ABC�ա�A��B��C�䣻
�ڡ�BAC��=��B��AC��
��l��ֱƽ��CC�䣻
��ֱ��BC��B��C��Ľ��㲻һ����l�ϣ�
��ȷ���У� ��
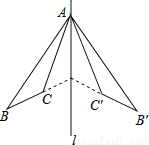
A. 4�� B. 3�� C. 2�� D. 1��
 B
����������������
�ߡ�ABC�͡�A��B��C�����ֱ��l�Գƣ�
��١�ABC�ա�A��B��C�䣬��ȷ��
�ڡ�BAC=��B��AC�䣬
���BAC+��CAC��=��B��AC��+��CAC�䣬
����BAC��=��B��AC��ȷ��
��l��ֱƽ��CC�䣬��ȷ��
��ӦΪ��ֱ��BC��B��C��Ľ���һ����l�ϣ��ʱ�С�����
����������������ȷ���Ǣ٢ڢ۹�3����
��...
B
����������������
�ߡ�ABC�͡�A��B��C�����ֱ��l�Գƣ�
��١�ABC�ա�A��B��C�䣬��ȷ��
�ڡ�BAC=��B��AC�䣬
���BAC+��CAC��=��B��AC��+��CAC�䣬
����BAC��=��B��AC��ȷ��
��l��ֱƽ��CC�䣬��ȷ��
��ӦΪ��ֱ��BC��B��C��Ľ���һ����l�ϣ��ʱ�С�����
����������������ȷ���Ǣ٢ڢ۹�3����
��... ��ͼ����һ������ֱ�������ΰ�ͼʾ��ʽ���η��ۣ�������˵����ȷ�ĸ����У� ��
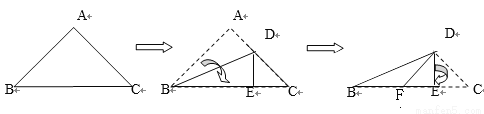
��DFƽ�֡�BDE���ڡ�BFD�ǵ��������Σ��ۡ�CED���ܳ�����BC�ij�
A. 1�� B. 2�� C. 3�� D. 0��
 B
��������������ԳƵ����ʼ��ɵó���.
��������
�ɶ�η��ۿɵã���DBE=��ABD=��ABC=��45��=22.5�㣬
��CDE =90�㣭��C =90�㣭45��=45��=��C��
��FDE=��CDE =45�㣬
���ABD=��EDB=��ADE=��(180�㣭��CDE) =��(180�㣭45��)=67. 5�㣬
���DFƽ�֡�BDE���������ȷ�Ļ�����BD...
B
��������������ԳƵ����ʼ��ɵó���.
��������
�ɶ�η��ۿɵã���DBE=��ABD=��ABC=��45��=22.5�㣬
��CDE =90�㣭��C =90�㣭45��=45��=��C��
��FDE=��CDE =45�㣬
���ABD=��EDB=��ADE=��(180�㣭��CDE) =��(180�㣭45��)=67. 5�㣬
���DFƽ�֡�BDE���������ȷ�Ļ�����BD... ��ͼ,��AOB��һ��P,�ֱ�P����OA��OB�ĶԳƵ�P1��P2��P1P2��OA��M,��OB��N,��P1P2=5cm,���PMN���ܳ�Ϊ_______.

 5cm
����������P��P1,P��P2����OA��OB�Գƣ�
��PM=P1M,PN=P2N��
���PMN���ܳ�=P1P2��
���PMN���ܳ���5 cm.
5cm
����������P��P1,P��P2����OA��OB�Գƣ�
��PM=P1M,PN=P2N��
���PMN���ܳ�=P1P2��
���PMN���ܳ���5 cm. �����������⣺��1������ijһֱ�߳���ԳƵ�����������ȫ�ȣ���2�����������εĶԳ����Ƕ��ǵ�ƽ���ߣ���3��һ���߶ε������˵�һ���ǹ��ھ������߶��е��ֱ�ߵĶԳƵ㣻��4���������������ȫ�ȣ���ô���ǹ���ijֱ�߳���Գơ�����������ĸ���Ϊ
A��0 B��1 C��2 D��3
 C
��������
�������������ƽ��ͼ�εĻ����������η�����С�⼴�������ж�.
��1������ijһֱ�߳���ԳƵ�����������ȫ�ȣ���3��һ���߶ε������˵�һ���ǹ��ھ������߶��е��ֱ�ߵĶԳƵ㣬��Ϊ�����⣻
��2�����������εĶԳ����Ƕ��ǵ�ƽ�������ڵ�ֱ�ߣ���4���������������ȫ�ȣ����ǿ�����ƽ�ƻ���ת���ɵģ���Ϊ�����⣻
��ѡC.
C
��������
�������������ƽ��ͼ�εĻ����������η�����С�⼴�������ж�.
��1������ijһֱ�߳���ԳƵ�����������ȫ�ȣ���3��һ���߶ε������˵�һ���ǹ��ھ������߶��е��ֱ�ߵĶԳƵ㣬��Ϊ�����⣻
��2�����������εĶԳ����Ƕ��ǵ�ƽ�������ڵ�ֱ�ߣ���4���������������ȫ�ȣ����ǿ�����ƽ�ƻ���ת���ɵģ���Ϊ�����⣻
��ѡC. ���ͬѧҪ֤�����⡰����Ա߷ֱ���ȵ��ı�����ƽ���ı��Ρ�����ȷ�ģ������ó߹���������ͼ1���ı���ABCD����д�������²���������֪����֤��
��֪����ͼ1�����ı���ABCD�У�BC=AD��AB=

��֤���ı���ABCD�� �ı��Σ�
��1���ڷ�������գ��Բ�ȫ��֪����֤��
��2�������ͬѧ��˼·д��֤�����̣�
��3��������������֤�����������.
 ��1������������2��������
�������������������1�����������Ϊ������Ա߷ֱ���ȵ��ı��Ρ��������ǡ���ƽ���ı��Ρ������ɵõ����ۣ�
��2������BD������SSS����֤����ABD�ա�CDB�ɵá�ADB=��DBC����ABD=��CDB�������ɵ�AB��CD��AD��CB����������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��οɵ��ı���ABCD��ƽ���ı��Σ�
��3�������⡰����Ա߷ֱ���ȵ��ı�����ƽ����...
��1������������2��������
�������������������1�����������Ϊ������Ա߷ֱ���ȵ��ı��Ρ��������ǡ���ƽ���ı��Ρ������ɵõ����ۣ�
��2������BD������SSS����֤����ABD�ա�CDB�ɵá�ADB=��DBC����ABD=��CDB�������ɵ�AB��CD��AD��CB����������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��οɵ��ı���ABCD��ƽ���ı��Σ�
��3�������⡰����Ա߷ֱ���ȵ��ı�����ƽ����... ���㣺 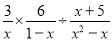 ��
��
 ��������������������ݷ�ʽ�˳���������㼴�ɣ�
���������ԭʽ==��
��������������������ݷ�ʽ�˳���������㼴�ɣ�
���������ԭʽ==�� 
