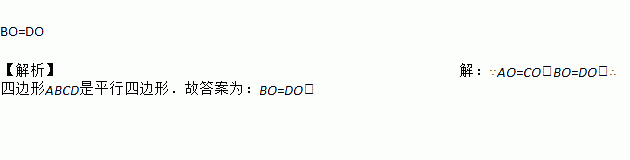题目内容
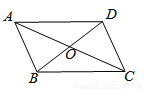
如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件_________
（只添一个即可），使四边形ABCD是平行四边形
BO=DO
【解析】【解析】
∵AO=CO，BO=DO，∴四边形ABCD是平行四边形．故答案为：BO=DO．
练习册系列答案
相关题目
从2，3，4，5，6中任取两个数就组成一组数，其中两数之和小于10的数组共有 组．
8
【解析】
试题分析：将所有情况列举出来，然后判断即可．
【解析】
从2，3，4，5，6中任取两个数就组成一组数，可能为2+3=5，2+4=6，2+5=7，2+6=8，3+4=7，3+5=8，3+6=9，4+5=9，4+6=10，5+6=11，
其中小于10的有8组，
故答案为：8． 如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P1、P2连P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长为_______.
5cm
【解析】∵P、P1,P、P2关于OA、OB对称，
∴PM=P1M,PN=P2N，
∴△PMN的周长=P1P2，
∴△PMN的周长是5 cm. 下列说法错误的是( )
A. 等边三角形是轴对称图形
B. 轴对称图形的对应边相等,对应角相等
C. 成轴对称的两条线段必在对称轴一侧
D. 成轴对称的两个图形对应点的连线被对称轴垂直平分
C
【解析】A. 由等边三角形的性质知,等边三角形是轴对称图形,正确;
B. 由轴对称的性质知,轴对称图形的对应边相等,对应角相等,正确;
C. 成轴对称的两条线段必在对称轴两侧,故错误;
D. 由轴对称的性质知,成轴对称的两个图形对应点的连线被对称轴垂直平分,正确;
故选C. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD，并写出了如下不完整的已知和求证．
已知：如图1，在四边形ABCD中，BC=AD，AB=
求证：四边形ABCD是 四边形．
（1）在方框中填空，以补全已知和求证；
（2）按嘉淇同学的思路写出证明过程；
（3）用文字叙述所证命题的逆命题.
（1）见解析；（2）见解析
【解析】试题分析：（1）命题的题设为“两组对边分别相等的四边形”，结论是“是平行四边形”，即可得到结论；
（2）连接BD，利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC，∠ABD=∠CDB，进而可得AB∥CD，AD∥CB，根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形；
（3）把命题“两组对边分别相等的四边形是平行四... 在下列条件中，不能确定四边形ABCD为平行四边形的是（ ）
A. ∠A=∠C，∠B=∠D B. ∠A=∠B=∠C=90°
C. ∠A+∠B=180°，∠B+∠C=180° D. ∠A+∠B=180°，∠C+∠D=180°
D
【解析】试题分析：A．∠A=∠C，∠B=∠D，能判定四边形ABCD是平行四边形；
B．∠A=∠B=∠C=90°，能判定四边形ABCD是平行四边形；
C．∠A+∠B=180°，∠B+∠C=180°，能判定四边形ABCD是平行四边形；
D．∠A+∠B=180°，∠C+∠D=180°，不能判定四边形ABCD是平行四边形．
故选D． 已知四边形
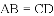
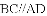
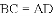
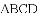
A. 6种 B. 5种 C. 4种 D. 3种
C
【解析】平行四边形的判定，平行四边形的判定方法共有五种，在四边形中如果有：
1、四边形的两组对边分别平行；
2、一组对边平行且相等；
3、两组对边分别相等；
4、对角线互相平分；
5、两组对角分别相等．则四边形是平行四边形
根据平行四边形的判定，符合条件的有4种，分别是：①②、③④、②③、①④．
故选C 下列事件中,是必然事件的是( )
A. 两条线段可以组成一个三角形
B. 400人中有两个人的生日在同一天
C. 早上的太阳从西方升起
D. 打开电视机,它正在播放动画片
B
【解析】试题解析：A. 两条线段可以组成一个三角形是不可能事件，故错误；
B.400人中有两个人的生日在同一天是必然事件，故正确；
C. 早上的太阳从西方升起是不可能事件，故错误；
D. 打开电视机，它正在播放动画片是随机事件，故错误；
故选B. 计算：
＝_______
【解析】试题分析：原式＝＝＝＝．
故答案为： ．