��Ŀ����
(������������ĩ)��ͼ�����ı���ABCD�У�AB��DC��AD��BC��5��DC��7��AB��13����P�ӵ�A������3����λ/s���ٶ���AD��DC���յ�C�˶���ͬʱ��Q�ӵ�B��������1����λ/s���ٶ���BA���յ�A�˶������ı���PQBCΪƽ���ı���ʱ���˶�ʱ��Ϊ(����)
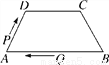
A. 4s B. 3s C. 2s D. 1s
 B
��������������������˶�ʱ��Ϊt�룬��CP=12-3t��BQ=t��
��������õ�12-3t=t��
��ã�t=3��
��ѡB��
B
��������������������˶�ʱ��Ϊt�룬��CP=12-3t��BQ=t��
��������õ�12-3t=t��
��ã�t=3��
��ѡB��
���в��ȹ�ϵһ����ȷ���ǣ� ��
A.|a|��0 B.��x2��0 C.��x+1��2��0 D.a2��0
 C
��������
������������ݾ���ֵ����ȫƽ��ʽ��������⣮
��������
A��|a|��0������
B����x2��0������
C����x+1��2��0����ȷ��
D��a2��0������
��ѡC��
C
��������
������������ݾ���ֵ����ȫƽ��ʽ��������⣮
��������
A��|a|��0������
B����x2��0������
C����x+1��2��0����ȷ��
D��a2��0������
��ѡC�� �����������⣺��1������ijһֱ�߳���ԳƵ�����������ȫ�ȣ���2�����������εĶԳ����Ƕ��ǵ�ƽ���ߣ���3��һ���߶ε������˵�һ���ǹ��ھ������߶��е��ֱ�ߵĶԳƵ㣻��4���������������ȫ�ȣ���ô���ǹ���ijֱ�߳���Գơ�����������ĸ���Ϊ
A��0 B��1 C��2 D��3
 C
��������
�������������ƽ��ͼ�εĻ����������η�����С�⼴�������ж�.
��1������ijһֱ�߳���ԳƵ�����������ȫ�ȣ���3��һ���߶ε������˵�һ���ǹ��ھ������߶��е��ֱ�ߵĶԳƵ㣬��Ϊ�����⣻
��2�����������εĶԳ����Ƕ��ǵ�ƽ�������ڵ�ֱ�ߣ���4���������������ȫ�ȣ����ǿ�����ƽ�ƻ���ת���ɵģ���Ϊ�����⣻
��ѡC.
C
��������
�������������ƽ��ͼ�εĻ����������η�����С�⼴�������ж�.
��1������ijһֱ�߳���ԳƵ�����������ȫ�ȣ���3��һ���߶ε������˵�һ���ǹ��ھ������߶��е��ֱ�ߵĶԳƵ㣬��Ϊ�����⣻
��2�����������εĶԳ����Ƕ��ǵ�ƽ�������ڵ�ֱ�ߣ���4���������������ȫ�ȣ����ǿ�����ƽ�ƻ���ת���ɵģ���Ϊ�����⣻
��ѡC. ���ͬѧҪ֤�����⡰����Ա߷ֱ���ȵ��ı�����ƽ���ı��Ρ�����ȷ�ģ������ó߹���������ͼ1���ı���ABCD����д�������²���������֪����֤��
��֪����ͼ1�����ı���ABCD�У�BC=AD��AB=

��֤���ı���ABCD�� �ı��Σ�
��1���ڷ�������գ��Բ�ȫ��֪����֤��
��2�������ͬѧ��˼·д��֤�����̣�
��3��������������֤�����������.
 ��1������������2��������
�������������������1�����������Ϊ������Ա߷ֱ���ȵ��ı��Ρ��������ǡ���ƽ���ı��Ρ������ɵõ����ۣ�
��2������BD������SSS����֤����ABD�ա�CDB�ɵá�ADB=��DBC����ABD=��CDB�������ɵ�AB��CD��AD��CB����������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��οɵ��ı���ABCD��ƽ���ı��Σ�
��3�������⡰����Ա߷ֱ���ȵ��ı�����ƽ����...
��1������������2��������
�������������������1�����������Ϊ������Ա߷ֱ���ȵ��ı��Ρ��������ǡ���ƽ���ı��Ρ������ɵõ����ۣ�
��2������BD������SSS����֤����ABD�ա�CDB�ɵá�ADB=��DBC����ABD=��CDB�������ɵ�AB��CD��AD��CB����������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��οɵ��ı���ABCD��ƽ���ı��Σ�
��3�������⡰����Ա߷ֱ���ȵ��ı�����ƽ����... ��ͼ,��֪��ABC������A��CΪԲ�ģ�BC��AB��Ϊ�뾶������������ֱ��BC�Ϸ����ڵ�D������AD��CD������( )
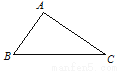
A. ��ADC���BAD��� B. ��ADC���BAD����
C. ��ADC���ABC���� D. ��ADC���ABC����
 B
����������ͼ���������AD=BC��CD=AB�����ı���ABCD��ƽ���ı��Σ����ADC+��BAD=180�㣬��ADC=��ABC����B��ȷ��
B
����������ͼ���������AD=BC��CD=AB�����ı���ABCD��ƽ���ı��Σ����ADC+��BAD=180�㣬��ADC=��ABC����B��ȷ�� ��֪�ı���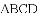
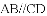
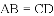
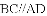
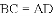
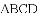
A. 6�� B. 5�� C. 4�� D. 3��
 C
��������ƽ���ı��ε��ж���ƽ���ı��ε��ж������������֣����ı���������У�
1���ı��ε�����Ա߷ֱ�ƽ�У�
2��һ��Ա�ƽ������ȣ�
3������Ա߷ֱ���ȣ�
4���Խ�����ƽ�֣�
5������ԽǷֱ���ȣ����ı�����ƽ���ı���
����ƽ���ı��ε��ж���������������4�֣��ֱ��ǣ��٢ڡ��ۢܡ��ڢۡ��٢ܣ�
��ѡC
C
��������ƽ���ı��ε��ж���ƽ���ı��ε��ж������������֣����ı���������У�
1���ı��ε�����Ա߷ֱ�ƽ�У�
2��һ��Ա�ƽ������ȣ�
3������Ա߷ֱ���ȣ�
4���Խ�����ƽ�֣�
5������ԽǷֱ���ȣ����ı�����ƽ���ı���
����ƽ���ı��ε��ж���������������4�֣��ֱ��ǣ��٢ڡ��ۢܡ��ڢۡ��٢ܣ�
��ѡC �������¼�����Ϊ����,��˵�����ֱ�.
���������һ��ʯͷ,ʯͷ�����̫��;
�ڼס�������ͬѧ������ë�����,��ʤ;
�۴�һ���˿����������ȡһ����,�����������Ǻ���;
�ܺڰ��д�һ��Կ��������ѡ��һ��,���������˴���;
����������������0;
�������ǰ���,����ѡ��һ��ͬѧ,��ͬѧ������;
�������̫������������.
 �𰸼�����
��������������������¼����ƿɽ������ļ����¼�����Ϊ�������¼�������¼���Ȼ�����¼�������ȷ���ԣ��ɽ��¼���Ϊȷ���¼��Ͳ�ȷ���¼����ݴ˽��з��༴��.
��:���¼����ƻ���:�������¼�:�٢ݢ�;����¼�:�ڢۢܢ�.
�𰸼�����
��������������������¼����ƿɽ������ļ����¼�����Ϊ�������¼�������¼���Ȼ�����¼�������ȷ���ԣ��ɽ��¼���Ϊȷ���¼��Ͳ�ȷ���¼����ݴ˽��з��༴��.
��:���¼����ƻ���:�������¼�:�٢ݢ�;����¼�:�ڢۢܢ�. ���㣺 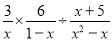 ��
��
 ��������������������ݷ�ʽ�˳���������㼴�ɣ�
���������ԭʽ==��
��������������������ݷ�ʽ�˳���������㼴�ɣ�
���������ԭʽ==�� ���� �Ľ���ǣ� ��
�Ľ���ǣ� ��
A. 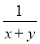 B.
B. 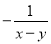 C.
C. 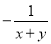 D.
D. 
 D
�����������������ԭʽ��
��
��
����
��ѡD��
D
�����������������ԭʽ��
��
��
����
��ѡD�� 
