题目内容
14.一个角的余角等于这个角的补角的$\frac{1}{3}$,则这个角为45°.分析 设这个角的度数是x,这个角的补角为180-x,余角为90-x.根据“一个角的余角等于这个角的补角的$\frac{1}{3}$”,列方程求解即可.
解答 解:设这个角的度数是x°,则
90-x=$\frac{1}{3}$(180-x),
解得x=45.
故答案为:45°.
点评 本题主要考查了余角和补角的概念以及运用.互为余角的两角的和为90°,互为补角的两角之和为180°.解此题的关键是能准确的从题中找出角之间的数量关系,从而计算出结果.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
4. 如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0,②4a-2b+c<0,③a-b+c=-9a,④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0,②4a-2b+c<0,③a-b+c=-9a,④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
 如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0,②4a-2b+c<0,③a-b+c=-9a,④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0,②4a-2b+c<0,③a-b+c=-9a,④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的是( )| A. | ①②③ | B. | ①③ | C. | ①④ | D. | ①③④ |
5.下列各组数据中的三个数,可作为三边长构成直角三角形的是( )
| A. | 0.2,0.3,0.4 | B. | 1,1,2 | C. | 6,6,6 | D. | 3,4,5 |
9.把(2-x)$\sqrt{\frac{1}{x-2}}$的根号外的(2-x)移入根号内得( )
| A. | $\sqrt{2-x}$ | B. | $\sqrt{x-2}$ | C. | -$\sqrt{2-x}$ | D. | -$\sqrt{x-2}$ |
19.下列说法中正确的是( )
| A. | 含有一个未知数的等式是一元一次方程 | |
| B. | 未知数的次数都是1次的方程是一元一次方程 | |
| C. | 含有一个未知数,并且未知数的次数都是一次的方程是一元一次方程 | |
| D. | 2t-7=1是一元一次方程 |
4.整数m满足$\left\{\begin{array}{l}{2m-1>0}\\{4-2m>-1}\end{array}\right.$,则关于x的方程m2x2-4x-2=(m+2)x2+3x+4的解为( )
| A. | x1=-2,x2=-$\frac{3}{2}$ | B. | x1=2,x2=$\frac{3}{2}$ | ||
| C. | x1=-$\frac{6}{7}$ | D. | x1=-2,x2=-$\frac{3}{2}$,x3=-$\frac{6}{7}$ |
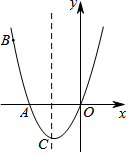 如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.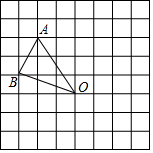 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.